Question Number 122748 by bemath last updated on 19/Nov/20
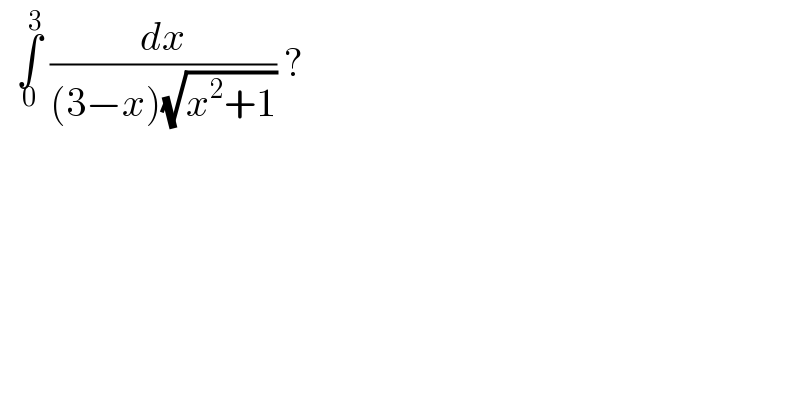
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{{dx}}{\left(\mathrm{3}−{x}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:? \\ $$
Answered by MJS_new last updated on 19/Nov/20
![∫(dx/((3−x)(√(x^2 +1))))= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))] =−2∫(dt/(t^2 −6t−1))=−2∫(dt/((t−3+(√(10)))(t−3+(√(10)))))= =((√(10))/(10))∫((1/(t−3+(√(10))))−(1/(t−3−(√(10)))))dt= =((√(10))/(10))ln ((t−3+(√(10)))/(t−3−(√(10)))) = =((√(10))/(10))ln ∣(( 3x+1+(√(10(x^2 +1))))/(3−x))∣ +C ∫_0 ^3 ... doesn′t converge](https://www.tinkutara.com/question/Q122752.png)
$$\int\frac{{dx}}{\left(\mathrm{3}−{x}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right] \\ $$$$=−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{6}{t}−\mathrm{1}}=−\mathrm{2}\int\frac{{dt}}{\left({t}−\mathrm{3}+\sqrt{\mathrm{10}}\right)\left({t}−\mathrm{3}+\sqrt{\mathrm{10}}\right)}= \\ $$$$=\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}\int\left(\frac{\mathrm{1}}{{t}−\mathrm{3}+\sqrt{\mathrm{10}}}−\frac{\mathrm{1}}{{t}−\mathrm{3}−\sqrt{\mathrm{10}}}\right){dt}= \\ $$$$=\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}\mathrm{ln}\:\frac{{t}−\mathrm{3}+\sqrt{\mathrm{10}}}{{t}−\mathrm{3}−\sqrt{\mathrm{10}}}\:= \\ $$$$=\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}\mathrm{ln}\:\mid\frac{\:\mathrm{3}{x}+\mathrm{1}+\sqrt{\mathrm{10}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}{\mathrm{3}−{x}}\mid\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}…\:\mathrm{doesn}'\mathrm{t}\:\mathrm{converge} \\ $$
Answered by liberty last updated on 19/Nov/20
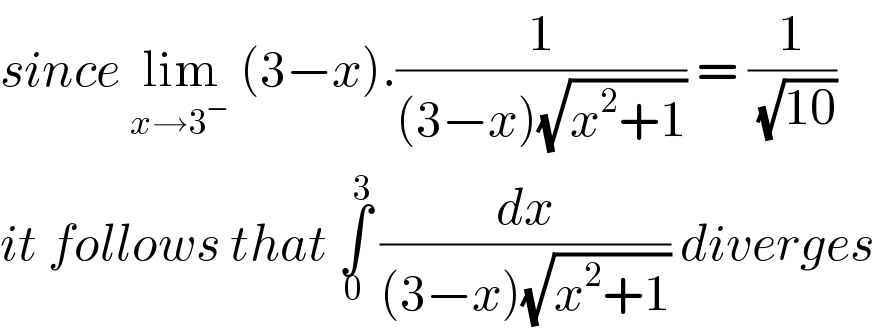
$${since}\:\underset{{x}\rightarrow\mathrm{3}^{−} } {\mathrm{lim}}\:\left(\mathrm{3}−{x}\right).\frac{\mathrm{1}}{\left(\mathrm{3}−{x}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}} \\ $$$${it}\:{follows}\:{that}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{{dx}}{\left(\mathrm{3}−{x}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:{diverges} \\ $$
Answered by Bird last updated on 19/Nov/20
![A =∫_0 ^3 (dx/((3−x)(√(x^2 +1)))) we do the changement x=sht ⇒ A =∫_0 ^(argsh(3)) ((cht)/((3−sht)cht))dt =∫_0 ^(ln(3+(√(10)))) (dt/(3−((e^t −e^(−t) )/2))) =∫_0 ^(ln(3+(√(10)))) ((2dt)/(6−e^t +e^(−t) )) =_(e^t =x) ∫_1 ^(3+(√(10))) ((2dx)/(x(6−x+x^(−1) ))) =2 ∫_1 ^(3+(√(10))) (dx/(6x−x^2 +1)) =−2∫_1 ^(3+(√(10))) (dx/(x^2 −6x−1)) Δ^′ =9+1=10 ⇒x_1 =3+(√(10)) x_2 =3−(√(10)) ⇒ I =−2 ∫_1 ^(3+(√(10))) (dx/((x−3−(√(10)))(x−3+(√(10))))) =−(2/(2(√(10)))) ∫_1 ^(3+(√(10))) ((1/(x−3−(√(10))))−(1/(x−3+(√(10)))))dx =−(1/( (√(10))))[ln∣((x−3−(√(10)))/(x−3+(√(10))))∣]_1 ^(3+(√(10))) =−∞ this integral dkverges..(√!)](https://www.tinkutara.com/question/Q122811.png)
$${A}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{{dx}}{\left(\mathrm{3}−{x}\right)\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\:{we}\:{do}\:{the} \\ $$$${changement}\:{x}={sht}\:\Rightarrow \\ $$$${A}\:=\int_{\mathrm{0}} ^{{argsh}\left(\mathrm{3}\right)} \:\:\frac{{cht}}{\left(\mathrm{3}−{sht}\right){cht}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}+\sqrt{\mathrm{10}}\right)} \:\:\:\:\frac{{dt}}{\mathrm{3}−\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}+\sqrt{\mathrm{10}}\right)} \:\frac{\mathrm{2}{dt}}{\mathrm{6}−{e}^{{t}} \:+{e}^{−{t}} } \\ $$$$=_{{e}^{{t}} \:={x}} \:\:\:\:\int_{\mathrm{1}} ^{\mathrm{3}+\sqrt{\mathrm{10}}} \:\:\:\:\frac{\mathrm{2}{dx}}{{x}\left(\mathrm{6}−{x}+{x}^{−\mathrm{1}} \right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\mathrm{3}+\sqrt{\mathrm{10}}} \:\:\:\:\:\frac{{dx}}{\mathrm{6}{x}−{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=−\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{3}+\sqrt{\mathrm{10}}} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{1}} \\ $$$$\Delta^{'} \:=\mathrm{9}+\mathrm{1}=\mathrm{10}\:\Rightarrow{x}_{\mathrm{1}} =\mathrm{3}+\sqrt{\mathrm{10}} \\ $$$${x}_{\mathrm{2}} =\mathrm{3}−\sqrt{\mathrm{10}}\:\Rightarrow \\ $$$${I}\:=−\mathrm{2}\:\int_{\mathrm{1}} ^{\mathrm{3}+\sqrt{\mathrm{10}}} \:\:\:\:\frac{{dx}}{\left({x}−\mathrm{3}−\sqrt{\mathrm{10}}\right)\left({x}−\mathrm{3}+\sqrt{\mathrm{10}}\right)} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{10}}}\:\int_{\mathrm{1}} ^{\mathrm{3}+\sqrt{\mathrm{10}}} \:\:\:\left(\frac{\mathrm{1}}{{x}−\mathrm{3}−\sqrt{\mathrm{10}}}−\frac{\mathrm{1}}{{x}−\mathrm{3}+\sqrt{\mathrm{10}}}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\left[{ln}\mid\frac{{x}−\mathrm{3}−\sqrt{\mathrm{10}}}{{x}−\mathrm{3}+\sqrt{\mathrm{10}}}\mid\right]_{\mathrm{1}} ^{\mathrm{3}+\sqrt{\mathrm{10}}} \:=−\infty \\ $$$${this}\:{integral}\:{dkverges}..\sqrt{!} \\ $$
