Menu Close

Question-136693

Tinku Tara 0 Comments
Pin




Question Number 136693 by liberty last updated on 25/Mar/21
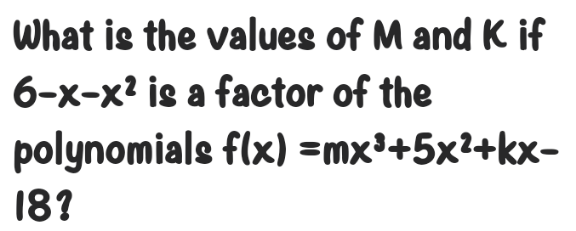
Commented by Olaf last updated on 25/Mar/21
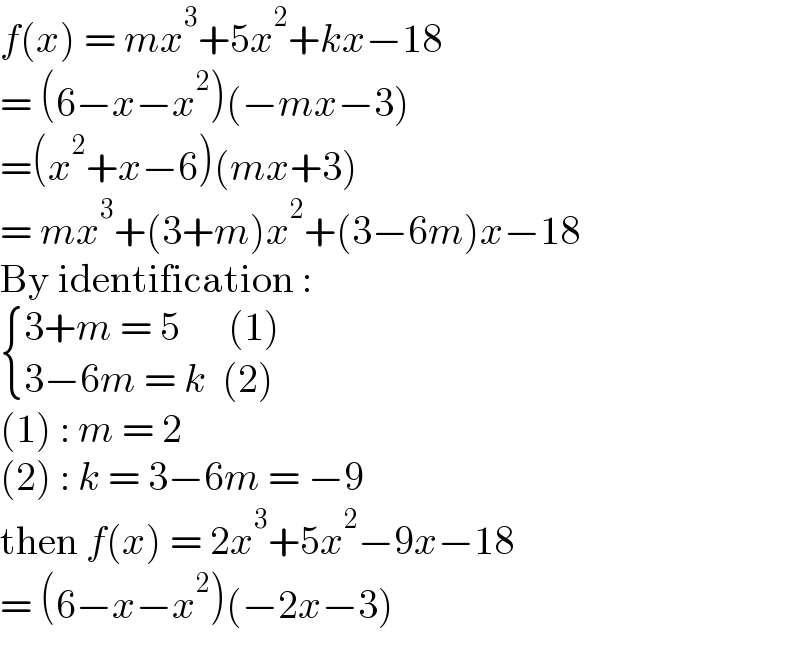
f(x) = mx^3 +5x^2 +kx−18 = (6−x−x^2 )(−mx−3) =(x^2 +x−6)(mx+3) = mx^3 +(3+m)x^2 +(3−6m)x−18 By identification : { ((3+m = 5 (1))),((3−6m = k (2))) :} (1) : m = 2 (2) : k = 3−6m = −9 then f(x) = 2x^3 +5x^2 −9x−18 = (6−x−x^2 )(−2x−3)
$${f}\left({x}\right)\:=\:{mx}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +{kx}−\mathrm{18} \\ $$$$=\:\left(\mathrm{6}−{x}−{x}^{\mathrm{2}} \right)\left(−{mx}−\mathrm{3}\right) \\ $$$$=\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)\left({mx}+\mathrm{3}\right) \\ $$$$=\:{mx}^{\mathrm{3}} +\left(\mathrm{3}+{m}\right){x}^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{6}{m}\right){x}−\mathrm{18} \\ $$$$\mathrm{By}\:\mathrm{identification}\:: \\ $$$$\begin{cases}{\mathrm{3}+{m}\:=\:\mathrm{5}\:\:\:\:\:\:\left(\mathrm{1}\right)}\\{\mathrm{3}−\mathrm{6}{m}\:=\:{k}\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)\::\:{m}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\::\:{k}\:=\:\mathrm{3}−\mathrm{6}{m}\:=\:−\mathrm{9} \\ $$$$\mathrm{then}\:{f}\left({x}\right)\:=\:\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{18} \\ $$$$=\:\left(\mathrm{6}−{x}−{x}^{\mathrm{2}} \right)\left(−\mathrm{2}{x}−\mathrm{3}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 25/Mar/21
6−x−x^2 =−(x+3)(x−2) ∴ x+3 & x−2 are also factors of f(x) By synthetic division determinant (((2)),m,5,k,(−18)),(,,(2m),(4m+10),(8m+2k+20)),((−3)),m,(2m+5),(4m+k+10),(8m+2k+2=0_(4m+k=−1) )),(,,(−3m),(3m−15),),(,m,(−m+5),(7m+k−5=0),)) 4m+k=−1 7m+k=5 3m=6⇒m=2 k=5−7m=5−7(2)=−9
$$\mathrm{6}−{x}−{x}^{\mathrm{2}} =−\left({x}+\mathrm{3}\right)\left({x}−\mathrm{2}\right) \\ $$$$\therefore\:{x}+\mathrm{3}\:\&\:{x}−\mathrm{2}\:{are}\:{also}\:{factors}\:{of}\:{f}\left({x}\right) \\ $$$$\mathcal{B}{y}\:{synthetic}\:{division} \\ $$$$\begin{array}{|c|c|c|c|c|}{\left.\mathrm{2}\right)}&\hline{{m}}&\hline{\mathrm{5}}&\hline{{k}}&\hline{−\mathrm{18}}\\{}&\hline{}&\hline{\mathrm{2}{m}}&\hline{\mathrm{4}{m}+\mathrm{10}}&\hline{\mathrm{8}{m}+\mathrm{2}{k}+\mathrm{20}}\\{\left.−\mathrm{3}\right)}&\hline{{m}}&\hline{\mathrm{2}{m}+\mathrm{5}}&\hline{\mathrm{4}{m}+{k}+\mathrm{10}}&\hline{\underset{\mathrm{4}{m}+{k}=−\mathrm{1}} {\mathrm{8}{m}+\mathrm{2}{k}+\mathrm{2}=\mathrm{0}}}\\{}&\hline{}&\hline{−\mathrm{3}{m}}&\hline{\mathrm{3}{m}−\mathrm{15}}&\hline{}\\{}&\hline{{m}}&\hline{−{m}+\mathrm{5}}&\hline{\mathrm{7}{m}+{k}−\mathrm{5}=\mathrm{0}}&\hline{}\\\hline\end{array} \\ $$$$\mathrm{4}{m}+{k}=−\mathrm{1} \\ $$$$\mathrm{7}{m}+{k}=\mathrm{5} \\ $$$$\mathrm{3}{m}=\mathrm{6}\Rightarrow{m}=\mathrm{2} \\ $$$${k}=\mathrm{5}−\mathrm{7}{m}=\mathrm{5}−\mathrm{7}\left(\mathrm{2}\right)=−\mathrm{9} \\ $$
Answered by bramlexs22 last updated on 25/Mar/21
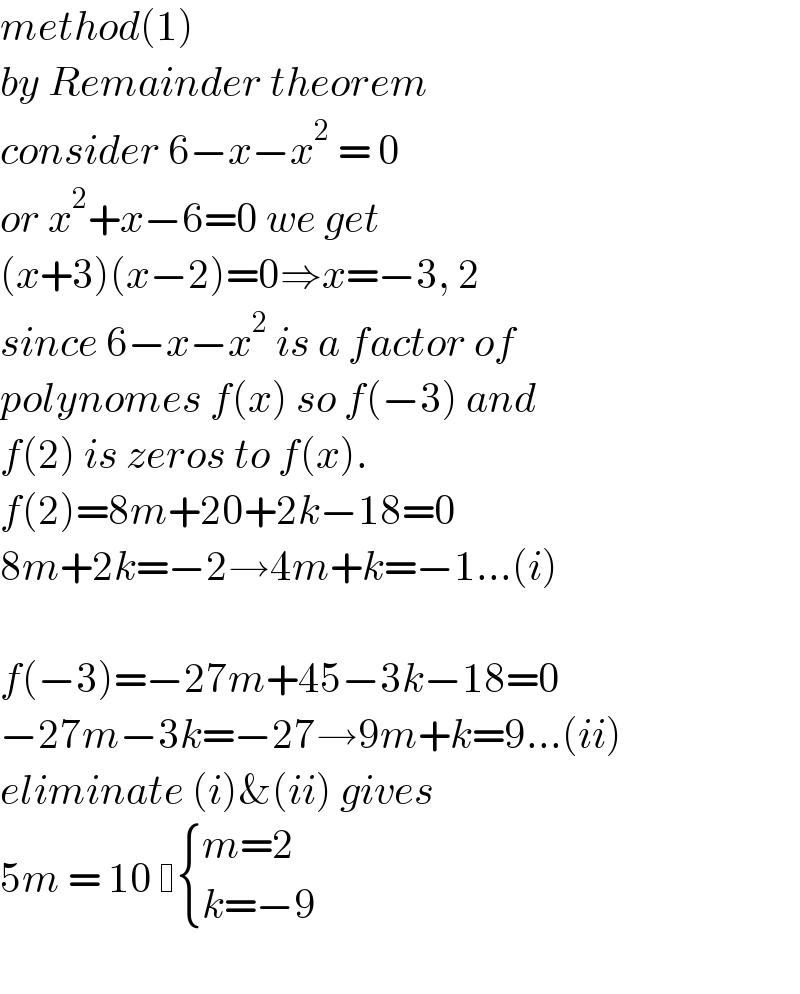
method(1) by Remainder theorem consider 6−x−x^2 = 0 or x^2 +x−6=0 we get (x+3)(x−2)=0⇒x=−3, 2 since 6−x−x^2 is a factor of polynomes f(x) so f(−3) and f(2) is zeros to f(x). f(2)=8m+20+2k−18=0 8m+2k=−2→4m+k=−1...(i) f(−3)=−27m+45−3k−18=0 −27m−3k=−27→9m+k=9...(ii) eliminate (i)&(ii) gives 5m = 10 { ((m=2)),((k=−9)) :}
$${method}\left(\mathrm{1}\right) \\ $$$${by}\:{Remainder}\:{theorem} \\ $$$${consider}\:\mathrm{6}−{x}−{x}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${or}\:{x}^{\mathrm{2}} +{x}−\mathrm{6}=\mathrm{0}\:{we}\:{get} \\ $$$$\left({x}+\mathrm{3}\right)\left({x}−\mathrm{2}\right)=\mathrm{0}\Rightarrow{x}=−\mathrm{3},\:\mathrm{2} \\ $$$${since}\:\mathrm{6}−{x}−{x}^{\mathrm{2}} \:{is}\:{a}\:{factor}\:{of} \\ $$$${polynomes}\:{f}\left({x}\right)\:{so}\:{f}\left(−\mathrm{3}\right)\:{and} \\ $$$${f}\left(\mathrm{2}\right)\:{is}\:{zeros}\:{to}\:{f}\left({x}\right). \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{8}{m}+\mathrm{20}+\mathrm{2}{k}−\mathrm{18}=\mathrm{0} \\ $$$$\mathrm{8}{m}+\mathrm{2}{k}=−\mathrm{2}\rightarrow\mathrm{4}{m}+{k}=−\mathrm{1}…\left({i}\right) \\ $$$$ \\ $$$${f}\left(−\mathrm{3}\right)=−\mathrm{27}{m}+\mathrm{45}−\mathrm{3}{k}−\mathrm{18}=\mathrm{0} \\ $$$$−\mathrm{27}{m}−\mathrm{3}{k}=−\mathrm{27}\rightarrow\mathrm{9}{m}+{k}=\mathrm{9}…\left({ii}\right) \\ $$$${eliminate}\:\left({i}\right)\&\left({ii}\right)\:{gives} \\ $$$$\mathrm{5}{m}\:=\:\mathrm{10}\: \begin{cases}{{m}=\mathrm{2}}\\{{k}=−\mathrm{9}}\end{cases} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *