Question Number 5630 by Rasheed Soomro last updated on 23/May/16

Commented by Rasheed Soomro last updated on 23/May/16

Commented by Yozzii last updated on 23/May/16

$${Let}\:{distance}\:{travelled}\:{be}\:{D}={d}_{\mathrm{1}} +{d}_{\mathrm{2}} . \\ $$$${Let}\:{x}\:{be}\:{the}\:{distance}\:{downstream}\: \\ $$$${where}\:{the}\:{man}\:{takes}\:{water}\:{from}\:{the} \\ $$$${river}\:{to}\:{the}\:{tent}.\:{Assuming}\:{the}\:{man}\:{runs}\:{along} \\ $$$${a}\:{straight}\:{line},\:{form}\:{a}\:{triangle}\:{ABC} \\ $$$${where}\:{AB}=\mathrm{200}\:{ft},{BC}=\left(\mathrm{450}−{x}\right){ft}, \\ $$$${AC}={d}_{\mathrm{1}} \:{and}\:{BC}\bot{AB}.\:{Thus},\:{by}\:{the}\:{Phythagorean}\:{theorem}, \\ $$$${d}_{\mathrm{1}} =\sqrt{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }. \\ $$$${In}\:{like}\:{manner},\:{d}_{\mathrm{2}} \:{is}\:{found}\:{to}\:{be}\: \\ $$$${d}_{\mathrm{2}} =\sqrt{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} }. \\ $$$$\therefore\:{D}=\sqrt{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }+\sqrt{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\therefore\:\frac{{dD}}{{dx}}=\frac{−\mathrm{0}.\mathrm{5}\left(\mathrm{2}\left(\mathrm{450}−{x}\right)\right)}{\:\sqrt{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }}+\frac{{x}}{\:\sqrt{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} }} \\ $$$$\frac{{dD}}{{dx}}=\frac{\sqrt{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} }\left({x}−\mathrm{450}\right)+{x}\sqrt{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }}{\:\sqrt{\left(\mathrm{200}^{\mathrm{2}} +\left(\mathrm{450}−{x}\right)^{\mathrm{2}} \right)\left(\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}} \\ $$$${At}\:{stationary}\:{points},\:\frac{{dD}}{{dx}}=\mathrm{0}. \\ $$$$\therefore\:{x}\sqrt{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }=\left(\mathrm{450}−{x}\right)\sqrt{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\sqrt{\frac{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} }}=\frac{\mathrm{450}−{x}}{{x}} \\ $$$$\therefore\frac{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} }{\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} }=\frac{\left(\mathrm{450}−{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} \left(\mathrm{450}−{x}\right)^{\mathrm{2}} +\mathrm{200}^{\mathrm{2}} {x}^{\mathrm{2}} =\left({x}−\mathrm{450}\right)^{\mathrm{2}} \left(\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} \right) \\ $$$$\left({x}−\mathrm{450}\right)^{\mathrm{2}} \left(\mathrm{100}^{\mathrm{2}} +{x}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)−\mathrm{200}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left\{\mathrm{100}\left({x}−\mathrm{450}\right)\right\}^{\mathrm{2}} −\left(\mathrm{200}{x}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{100}{x}−\mathrm{45000}−\mathrm{200}{x}\right)\left(\mathrm{100}{x}−\mathrm{45000}+\mathrm{200}{x}\right)=\mathrm{0} \\ $$$$\left(\mathrm{100}{x}+\mathrm{45000}\right)\left(\mathrm{300}{x}−\mathrm{45000}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{450}\right)\left({x}−\mathrm{150}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{150}\:{ft}\:{or}\:{x}=−\mathrm{450}\:{ft}. \\ $$$${But}\:{x}>\mathrm{0}.\:\therefore\:{x}\neq−\mathrm{450}{ft}\:{and}\:{x}=\mathrm{150}{ft}. \\ $$$${Let}\:{f}\left({x}\right)=\frac{{dD}}{{dx}}. \\ $$$${Then}\:{f}\left(\mathrm{149}.\mathrm{9}\right)\approx−\mathrm{2}.\mathrm{56}×\mathrm{10}^{−\mathrm{4}} \\ $$$${and}\:{f}\left(\mathrm{150}.\mathrm{1}\right)\approx\mathrm{2}.\mathrm{56}×\mathrm{10}^{−\mathrm{4}} . \\ $$$${Hence}\:{f}\left({x}\right)\:{increases}\:{for}\:{increasing} \\ $$$${x}\:{sufficiently}\:{close}\:{to}\:{x}=\mathrm{150}.\:{Thus} \\ $$$${at}\:{x}=\mathrm{150}\:{ft},\:{D}\:{takes}\:{a}\:{minimum}\:{value}. \\ $$
Commented by Rasheed Soomro last updated on 23/May/16

$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{x}\:\mathrm{you}\:\mathrm{calculated}\:\mathrm{is}\:\mathrm{correct}, \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{450}−\mathrm{x}=\mathrm{300}\:\mathrm{ft}\:\mathrm{upstream} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{location}\:\mathrm{of}\:\mathrm{hiker}. \\ $$$$\mathrm{Your}\:\mathrm{aproach}\:\mathrm{is}\:\mathrm{different}\:\mathrm{from}\:\mathrm{that}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{book}. \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{the}\:\mathrm{book},\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{river} \\ $$$$\mathrm{to}\:\mathrm{which}\:\mathrm{hiker}\:\:\mathrm{should}\:\mathrm{run}\:\mathrm{in}\:\mathrm{order}\:\mathrm{to}\:\mathrm{minimize} \\ $$$$\mathrm{the}\:\mathrm{distance}\:\mathrm{is}\:\mathrm{such}\:\mathrm{that}\:\mathrm{two}\:\mathrm{triangles}\:\mathrm{made}\:\mathrm{are} \\ $$$$\mathrm{similar}. \\ $$$$\mathrm{Anyway}\:\mathrm{I}\:\mathrm{Like}\:\mathrm{your}\:\mathrm{aproach}! \\ $$
Commented by Yozzii last updated on 23/May/16
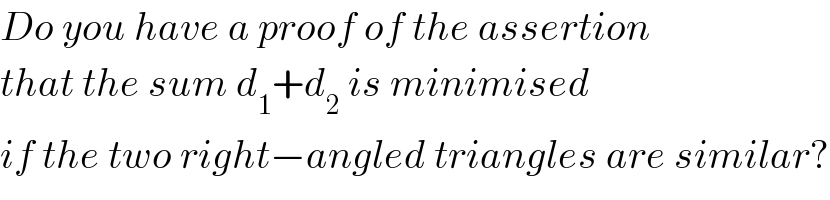
$${Do}\:{you}\:{have}\:{a}\:{proof}\:{of}\:{the}\:{assertion} \\ $$$${that}\:{the}\:{sum}\:{d}_{\mathrm{1}} +{d}_{\mathrm{2}} \:{is}\:{minimised} \\ $$$${if}\:{the}\:{two}\:{right}−{angled}\:{triangles}\:{are}\:{similar}? \\ $$
Commented by Rasheed Soomro last updated on 23/May/16

$$\mathrm{I}\:\mathrm{am}\:\mathrm{forwarding}\:\mathrm{the}\:\mathrm{explanation}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{book}\:\mathrm{regarding}\:\mathrm{your}\:\mathrm{request}. \\ $$
Commented by Rasheed Soomro last updated on 23/May/16

Commented by Rasheed Soomro last updated on 23/May/16

Commented by Yozzii last updated on 23/May/16

$${I}\:{see}.\:{Thanks}! \\ $$
