Question Number 122867 by bemath last updated on 20/Nov/20

Answered by som(math1967) last updated on 20/Nov/20
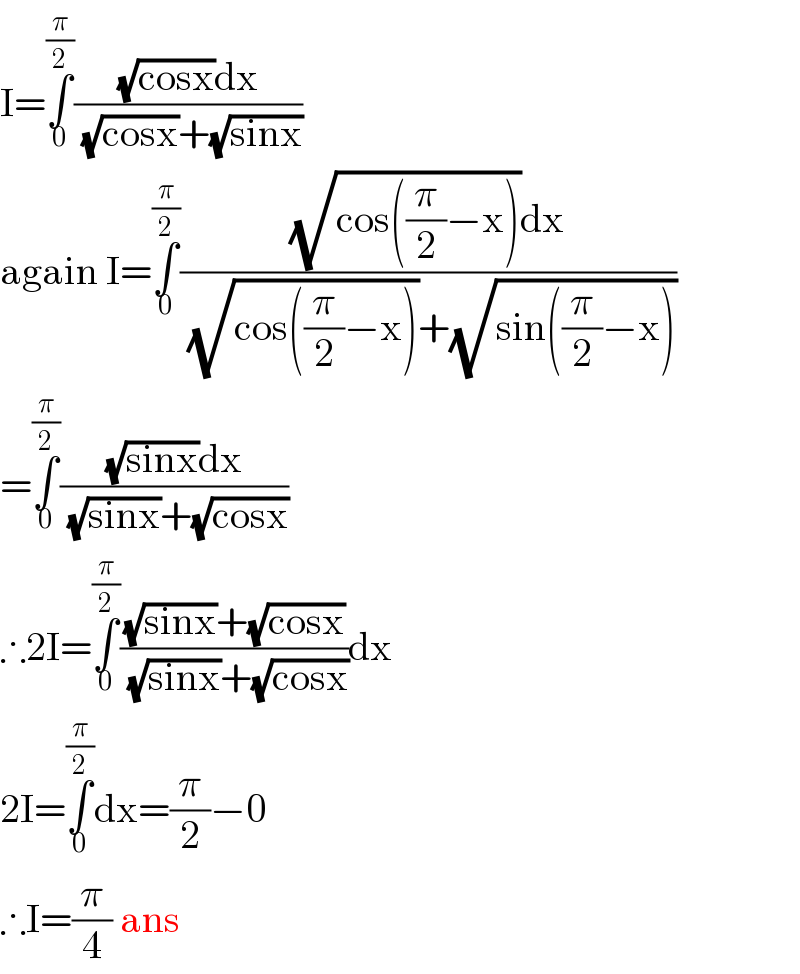
$$\mathrm{I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\sqrt{\mathrm{cosx}}\mathrm{dx}}{\:\sqrt{\mathrm{cosx}}+\sqrt{\mathrm{sinx}}} \\ $$$$\mathrm{again}\:\mathrm{I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\sqrt{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}\mathrm{dx}}{\:\sqrt{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}+\sqrt{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}} \\ $$$$=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\sqrt{\mathrm{sinx}}\mathrm{dx}}{\:\sqrt{\mathrm{sinx}}+\sqrt{\mathrm{cosx}}} \\ $$$$\therefore\mathrm{2I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\sqrt{\mathrm{sinx}}+\sqrt{\mathrm{cosx}}}{\:\sqrt{\mathrm{sinx}}+\sqrt{\mathrm{cosx}}}\mathrm{dx} \\ $$$$\mathrm{2I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{dx}=\frac{\pi}{\mathrm{2}}−\mathrm{0} \\ $$$$\therefore\mathrm{I}=\frac{\pi}{\mathrm{4}}\:\mathrm{ans} \\ $$
Answered by liberty last updated on 20/Nov/20
![φ =∫_0 ^(π/2) (1/(1+(√(tan x)))) dx using the interval inversion substitution that replaces x with (π/2)−x , we get φ =∫_0 ^(π/2) (1/(1+(√(cot x)))) dx = ∫_0 ^(π/2) ((√(tan x))/( (√(tan x)) +1)) dx adding together of φ(x) yields 2φ =∫_0 ^(π/2) (1/(1+(√(tan x)))) dx + ∫_0 ^(π/2) ((√(tan x))/(1+(√(tan x)))) dx 2φ = ∫_0 ^(π/2) dx = x ] _0^(π/2) φ = (π/4).](https://www.tinkutara.com/question/Q122876.png)
$$\phi\:=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}\:{dx}\: \\ $$$${using}\:{the}\:{interval}\:{inversion}\:{substitution} \\ $$$${that}\:{replaces}\:{x}\:{with}\:\frac{\pi}{\mathrm{2}}−{x}\:,\:{we}\:{get}\: \\ $$$$\phi\:=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{cot}\:{x}}}\:{dx}\:=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\sqrt{\mathrm{tan}\:{x}}}{\:\sqrt{\mathrm{tan}\:{x}}\:+\mathrm{1}}\:{dx} \\ $$$${adding}\:{together}\:{of}\:\phi\left({x}\right)\:{yields} \\ $$$$\mathrm{2}\phi\:=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}\:{dx}\:+\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}\:{dx} \\ $$$$\left.\mathrm{2}\phi\:=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:{dx}\:=\:{x}\:\right]\:_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\phi\:=\:\frac{\pi}{\mathrm{4}}.\: \\ $$
