Menu Close

Let-p-q-r-are-positive-real-numbers-0-lt-r-lt-min-p-q-Prove-that-p-r-q-r-min-pq-r-2-p-q-2r-

Tinku Tara 0 Comments
Pin




Question Number 71206 by naka3546 last updated on 13/Oct/19
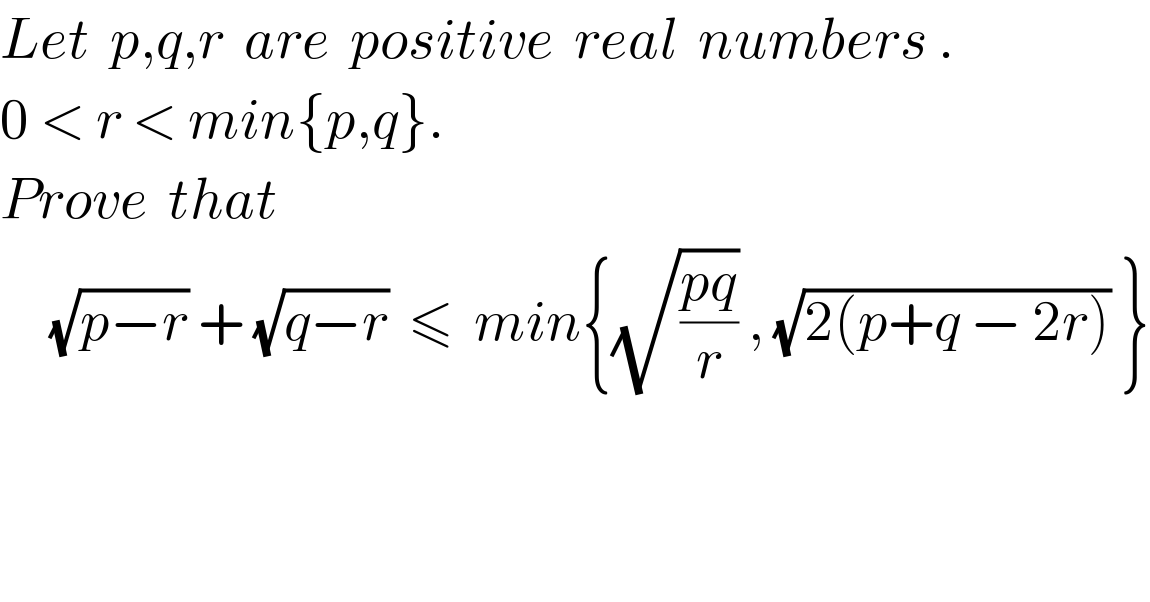
Let p,q,r are positive real numbers . 0 < r < min{p,q}. Prove that (√(p−r)) + (√(q−r)) ≤ min{(√((pq)/r)) , (√(2(p+q − 2r))) }
$${Let}\:\:{p},{q},{r}\:\:{are}\:\:{positive}\:\:{real}\:\:{numbers}\:. \\ $$$$\mathrm{0}\:<\:{r}\:<\:{min}\left\{{p},{q}\right\}. \\ $$$${Prove}\:\:{that} \\ $$$$\:\:\:\:\:\sqrt{{p}−{r}}\:+\:\sqrt{{q}−{r}}\:\:\leqslant\:\:{min}\left\{\sqrt{\frac{{pq}}{{r}}}\:,\:\sqrt{\mathrm{2}\left({p}+{q}\:−\:\mathrm{2}{r}\right)}\:\right\} \\ $$
Answered by mind is power last updated on 13/Oct/19
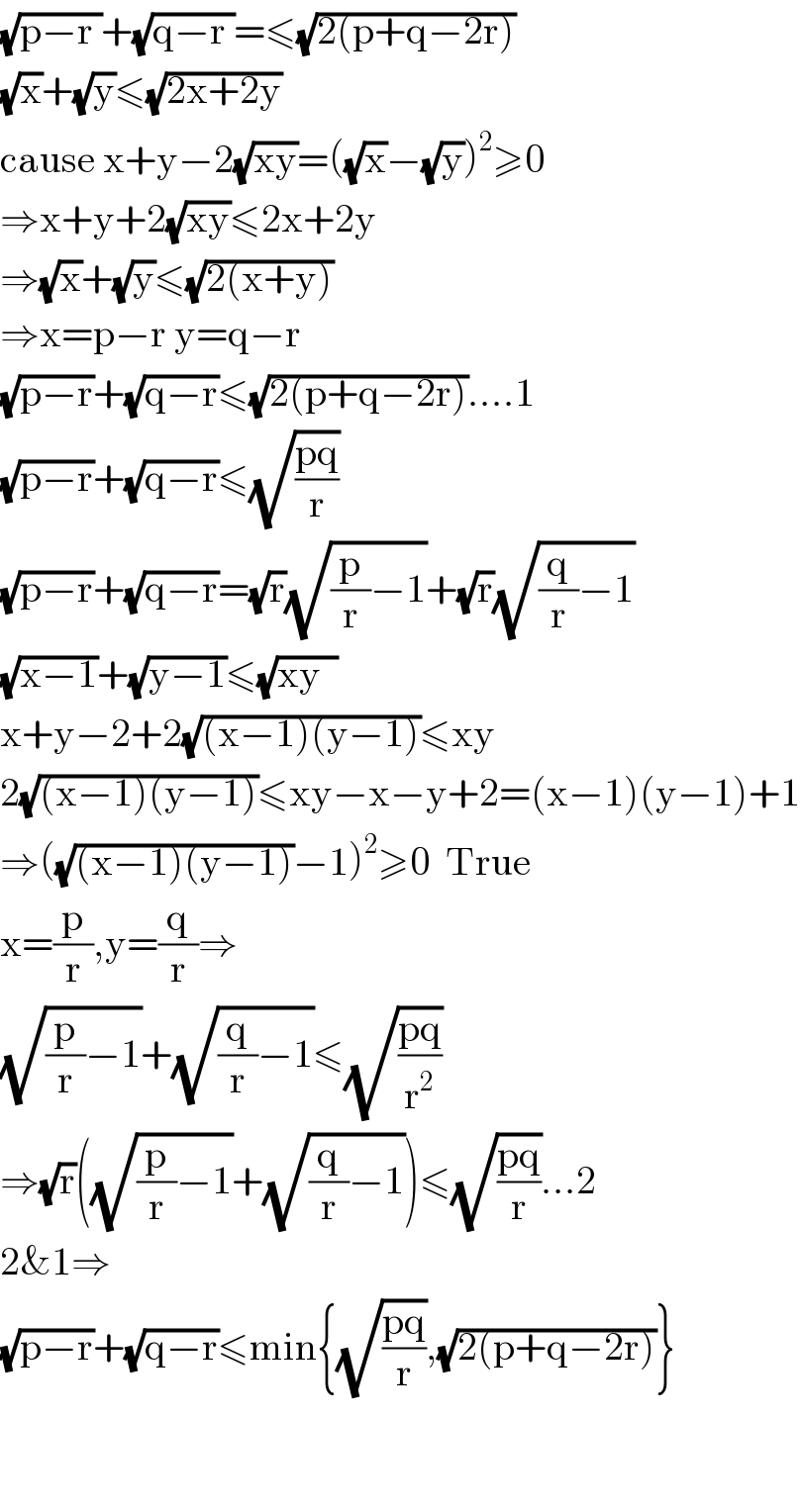
(√(p−r ))+(√(q−r ))=≤(√(2(p+q−2r))) (√x)+(√y)≤(√(2x+2y)) cause x+y−2(√(xy))=((√x)−(√y))^2 ≥0 ⇒x+y+2(√(xy))≤2x+2y ⇒(√x)+(√y)≤(√(2(x+y))) ⇒x=p−r y=q−r (√(p−r))+(√(q−r))≤(√(2(p+q−2r)))....1 (√(p−r))+(√(q−r))≤(√((pq)/r)) (√(p−r))+(√(q−r))=(√r)(√((p/r)−1))+(√r)(√((q/r)−1)) (√(x−1))+(√(y−1))≤(√(xy )) x+y−2+2(√((x−1)(y−1)))≤xy 2(√((x−1)(y−1)))≤xy−x−y+2=(x−1)(y−1)+1 ⇒((√((x−1)(y−1)))−1)^2 ≥0 True x=(p/r),y=(q/r)⇒ (√((p/r)−1))+(√((q/r)−1))≤(√((pq)/r^2 )) ⇒(√r)((√((p/r)−1))+(√((q/r)−1)))≤(√((pq)/r))...2 2&1⇒ (√(p−r))+(√(q−r))≤min{(√((pq)/r)),(√(2(p+q−2r)))}
$$\sqrt{\mathrm{p}−\mathrm{r}\:}+\sqrt{\mathrm{q}−\mathrm{r}\:}=\leqslant\sqrt{\mathrm{2}\left(\mathrm{p}+\mathrm{q}−\mathrm{2r}\right)} \\ $$$$\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}\leqslant\sqrt{\mathrm{2x}+\mathrm{2y}} \\ $$$$\mathrm{cause}\:\mathrm{x}+\mathrm{y}−\mathrm{2}\sqrt{\mathrm{xy}}=\left(\sqrt{\mathrm{x}}−\sqrt{\mathrm{y}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{y}+\mathrm{2}\sqrt{\mathrm{xy}}\leqslant\mathrm{2x}+\mathrm{2y} \\ $$$$\Rightarrow\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}\leqslant\sqrt{\mathrm{2}\left(\mathrm{x}+\mathrm{y}\right)} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{p}−\mathrm{r}\:\mathrm{y}=\mathrm{q}−\mathrm{r} \\ $$$$\sqrt{\mathrm{p}−\mathrm{r}}+\sqrt{\mathrm{q}−\mathrm{r}}\leqslant\sqrt{\mathrm{2}\left(\mathrm{p}+\mathrm{q}−\mathrm{2r}\right)}….\mathrm{1} \\ $$$$\sqrt{\mathrm{p}−\mathrm{r}}+\sqrt{\mathrm{q}−\mathrm{r}}\leqslant\sqrt{\frac{\mathrm{pq}}{\mathrm{r}}} \\ $$$$\sqrt{\mathrm{p}−\mathrm{r}}+\sqrt{\mathrm{q}−\mathrm{r}}=\sqrt{\mathrm{r}}\sqrt{\frac{\mathrm{p}}{\mathrm{r}}−\mathrm{1}}+\sqrt{\mathrm{r}}\sqrt{\frac{\mathrm{q}}{\mathrm{r}}−\mathrm{1}} \\ $$$$\sqrt{\mathrm{x}−\mathrm{1}}+\sqrt{\mathrm{y}−\mathrm{1}}\leqslant\sqrt{\mathrm{xy}\:\:} \\ $$$$\mathrm{x}+\mathrm{y}−\mathrm{2}+\mathrm{2}\sqrt{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{y}−\mathrm{1}\right)}\leqslant\mathrm{xy} \\ $$$$\mathrm{2}\sqrt{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{y}−\mathrm{1}\right)}\leqslant\mathrm{xy}−\mathrm{x}−\mathrm{y}+\mathrm{2}=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{y}−\mathrm{1}\right)+\mathrm{1} \\ $$$$\Rightarrow\left(\sqrt{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{y}−\mathrm{1}\right)}−\mathrm{1}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:\:\mathrm{True} \\ $$$$\mathrm{x}=\frac{\mathrm{p}}{\mathrm{r}},\mathrm{y}=\frac{\mathrm{q}}{\mathrm{r}}\Rightarrow \\ $$$$\sqrt{\frac{\mathrm{p}}{\mathrm{r}}−\mathrm{1}}+\sqrt{\frac{\mathrm{q}}{\mathrm{r}}−\mathrm{1}}\leqslant\sqrt{\frac{\mathrm{pq}}{\mathrm{r}^{\mathrm{2}} }} \\ $$$$\Rightarrow\sqrt{\mathrm{r}}\left(\sqrt{\frac{\mathrm{p}}{\mathrm{r}}−\mathrm{1}}+\sqrt{\frac{\mathrm{q}}{\mathrm{r}}−\mathrm{1}}\right)\leqslant\sqrt{\frac{\mathrm{pq}}{\mathrm{r}}}…\mathrm{2} \\ $$$$\mathrm{2\&1}\Rightarrow \\ $$$$\sqrt{\mathrm{p}−\mathrm{r}}+\sqrt{\mathrm{q}−\mathrm{r}}\leqslant\mathrm{min}\left\{\sqrt{\frac{\mathrm{pq}}{\mathrm{r}}},\sqrt{\mathrm{2}\left(\mathrm{p}+\mathrm{q}−\mathrm{2r}\right)}\right\} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *