Question Number 136761 by I want to learn more last updated on 25/Mar/21

Commented by I want to learn more last updated on 25/Mar/21

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by mr W last updated on 25/Mar/21
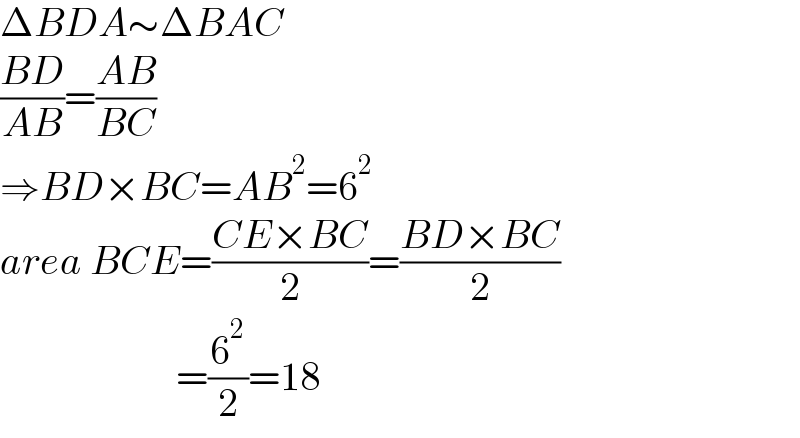
$$\Delta{BDA}\sim\Delta{BAC} \\ $$$$\frac{{BD}}{{AB}}=\frac{{AB}}{{BC}} \\ $$$$\Rightarrow{BD}×{BC}={AB}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} \\ $$$${area}\:{BCE}=\frac{{CE}×{BC}}{\mathrm{2}}=\frac{{BD}×{BC}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{18} \\ $$
Commented by I want to learn more last updated on 25/Mar/21
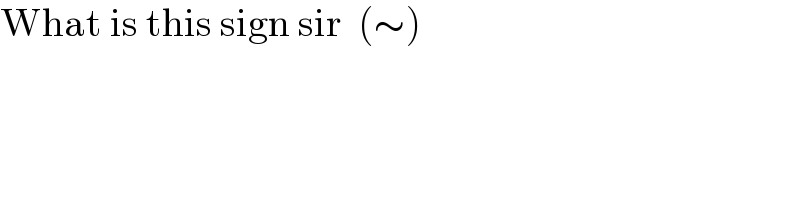
$$\mathrm{What}\:\mathrm{is}\:\mathrm{this}\:\mathrm{sign}\:\mathrm{sir}\:\:\left(\sim\right) \\ $$
Commented by mr W last updated on 25/Mar/21

$${not}\:{yet}\:{learnt}\:{geometry}\:{about} \\ $$$${similar}\:{triangles}?\:{then}\:{you}\:{can}\:{not} \\ $$$${understand}\:{the}\:{working}. \\ $$
Commented by I want to learn more last updated on 25/Mar/21
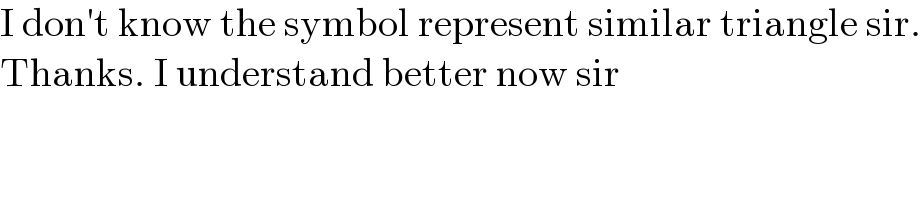
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{symbol}\:\mathrm{represent}\:\mathrm{similar}\:\mathrm{triangle}\:\mathrm{sir}. \\ $$$$\mathrm{Thanks}.\:\mathrm{I}\:\mathrm{understand}\:\mathrm{better}\:\mathrm{now}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 25/Mar/21

$${which}\:{symbol}\:{do}\:{you}\:{use}\:{otherwise}? \\ $$
Commented by I want to learn more last updated on 25/Mar/21

$$\mathrm{I}\:\mathrm{understand}\:\mathrm{better}\:\mathrm{now}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 25/Mar/21
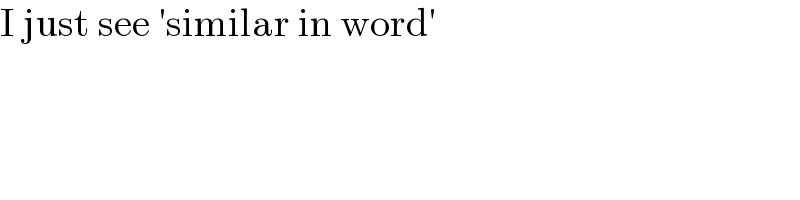
$$\mathrm{I}\:\mathrm{just}\:\mathrm{see}\:'\mathrm{similar}\:\mathrm{in}\:\mathrm{word}' \\ $$
Commented by mr W last updated on 26/Mar/21

$${i}\:{thought}\:{in}\:{all}\:{world}\:{the}\:{symbol}\:\sim\: \\ $$$${is}\:{used}\:{for}\:{similarity}\:{in}\:{geometry}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 27/Mar/21

$$\mathrm{thanks}\:\mathrm{prof} \\ $$
