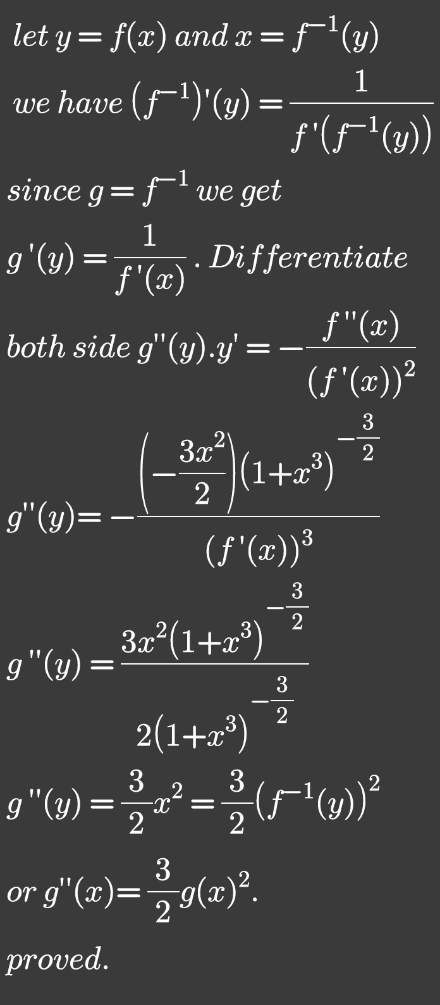Question Number 123410 by bemath last updated on 25/Nov/20
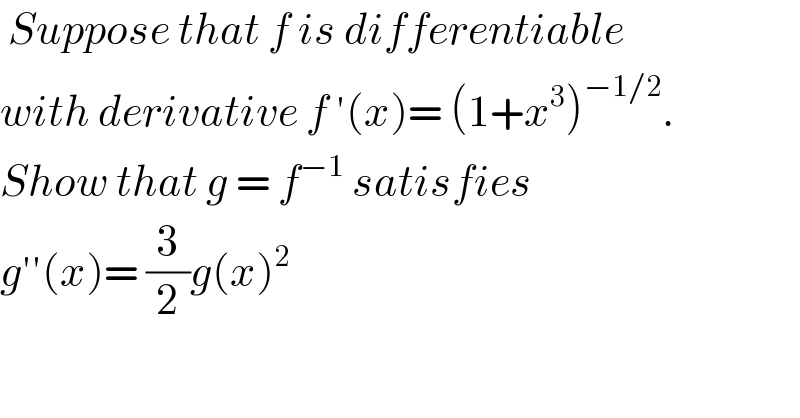
$$\:{Suppose}\:{that}\:{f}\:{is}\:{differentiable} \\ $$$${with}\:{derivative}\:{f}\:'\left({x}\right)=\:\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{−\mathrm{1}/\mathrm{2}} . \\ $$$${Show}\:{that}\:{g}\:=\:{f}^{−\mathrm{1}} \:{satisfies}\: \\ $$$${g}''\left({x}\right)=\:\frac{\mathrm{3}}{\mathrm{2}}{g}\left({x}\right)^{\mathrm{2}} \\ $$
Answered by mnjuly1970 last updated on 25/Nov/20
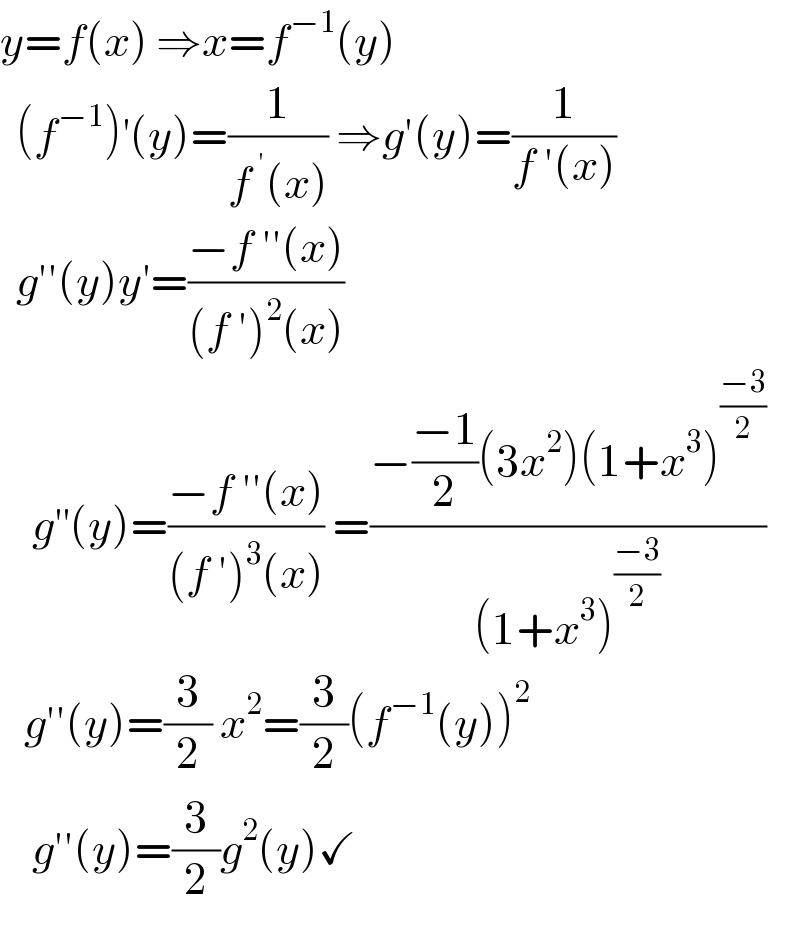
$${y}={f}\left({x}\right)\:\Rightarrow{x}={f}^{−\mathrm{1}} \left({y}\right) \\ $$$$\:\:\left({f}^{−\mathrm{1}} \right)^{'} \left({y}\right)=\frac{\mathrm{1}}{{f}^{\:'} \left({x}\right)}\:\Rightarrow{g}'\left({y}\right)=\frac{\mathrm{1}}{{f}\:'\left({x}\right)} \\ $$$$\:\:{g}''\left({y}\right){y}^{'} =\frac{−{f}\:''\left({x}\right)}{\left({f}\:'\right)^{\mathrm{2}} \left({x}\right)}\: \\ $$$$\:\:\:\:{g}^{''} \left({y}\right)=\frac{−{f}\:''\left({x}\right)}{\left({f}\:'\right)^{\mathrm{3}} \left({x}\right)}\:=\frac{−\frac{−\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{−\mathrm{3}}{\mathrm{2}}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{−\mathrm{3}}{\mathrm{2}}} } \\ $$$$\:\:\:{g}''\left({y}\right)=\frac{\mathrm{3}}{\mathrm{2}}\:{x}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}}\left({f}^{−\mathrm{1}} \left({y}\right)\right)^{\mathrm{2}} \\ $$$$\:\:\:\:{g}''\left({y}\right)=\frac{\mathrm{3}}{\mathrm{2}}{g}^{\mathrm{2}} \left({y}\right)\checkmark \\ $$
Commented by bemath last updated on 25/Nov/20