Question Number 123551 by joki last updated on 26/Nov/20

Answered by ebi last updated on 26/Nov/20
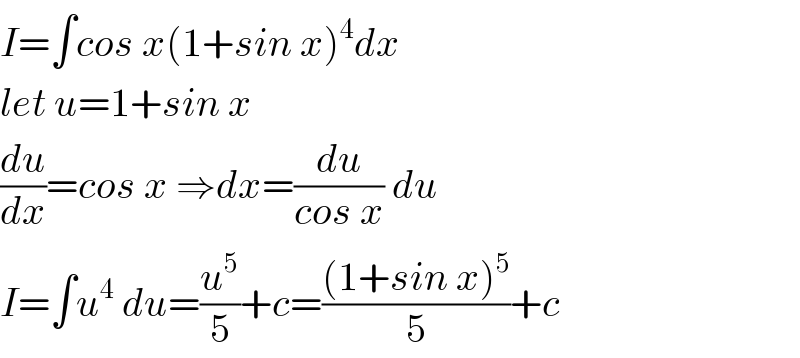
$${I}=\int{cos}\:{x}\left(\mathrm{1}+{sin}\:{x}\right)^{\mathrm{4}} {dx} \\ $$$${let}\:{u}=\mathrm{1}+{sin}\:{x} \\ $$$$\frac{{du}}{{dx}}={cos}\:{x}\:\Rightarrow{dx}=\frac{{du}}{{cos}\:{x}}\:{du} \\ $$$${I}=\int{u}^{\mathrm{4}} \:{du}=\frac{{u}^{\mathrm{5}} }{\mathrm{5}}+{c}=\frac{\left(\mathrm{1}+{sin}\:{x}\right)^{\mathrm{5}} }{\mathrm{5}}+{c} \\ $$
Commented by joki last updated on 26/Nov/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Olaf last updated on 26/Nov/20
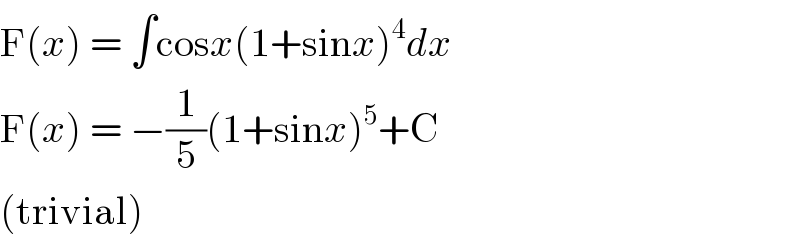
$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{cos}{x}\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{4}} {dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{5}} +\mathrm{C} \\ $$$$\left(\mathrm{trivial}\right) \\ $$
Commented by joki last updated on 26/Nov/20

$${thank}\:{you}\:{sir} \\ $$
