Question Number 123595 by Snail last updated on 26/Nov/20
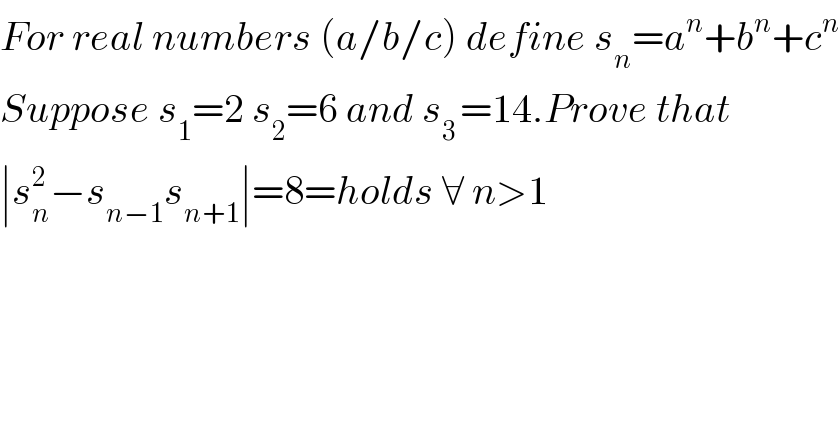
$${For}\:{real}\:{numbers}\:\left({a}/{b}/{c}\right)\:{define}\:{s}_{{n}} ={a}^{{n}} +{b}^{{n}} +{c}^{{n}} \\ $$$${Suppose}\:{s}_{\mathrm{1}} =\mathrm{2}\:{s}_{\mathrm{2}} =\mathrm{6}\:{and}\:{s}_{\mathrm{3}\:} =\mathrm{14}.{Prove}\:{that}\: \\ $$$$\mid{s}_{{n}} ^{\mathrm{2}} −{s}_{{n}−\mathrm{1}} {s}_{{n}+\mathrm{1}} \mid=\mathrm{8}={holds}\:\forall\:{n}>\mathrm{1} \\ $$
Commented by Snail last updated on 26/Nov/20

$$ \\ $$$$ \\ $$$${I}\:{had}\:{tried}\:{using}\:{Mathematical}\:\:{Induction}\:{but}\:{unabld}\:{to}\:{solve} \\ $$$$ \\ $$
