Question Number 469 by 123456 last updated on 25/Jan/15

$${proof}\:{or}\:{given}\:{a}\:{counter}−{example} \\ $$$${if}\:{p}\:{is}\:{prime}\:{and}\:{a}\in\mathbb{N}\:{then} \\ $$$${p}\mid\left({a}+{p}\right)^{{p}} −{a}^{{p}} \\ $$
Answered by prakash jain last updated on 10/Jan/15
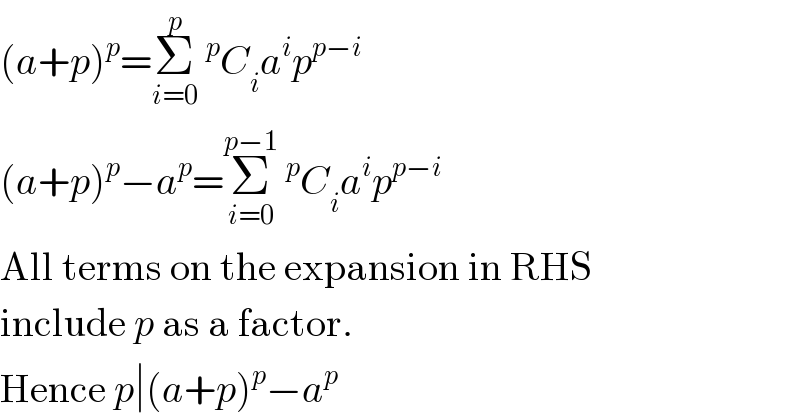
$$\left({a}+{p}\right)^{{p}} =\underset{{i}=\mathrm{0}} {\overset{{p}} {\sum}}\:^{{p}} {C}_{{i}} {a}^{{i}} {p}^{{p}−{i}} \\ $$$$\left({a}+{p}\right)^{{p}} −{a}^{{p}} =\underset{{i}=\mathrm{0}} {\overset{{p}−\mathrm{1}} {\sum}}\:^{{p}} {C}_{{i}} {a}^{{i}} {p}^{{p}−{i}} \\ $$$$\mathrm{All}\:\mathrm{terms}\:\mathrm{on}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{in}\:\mathrm{RHS} \\ $$$$\mathrm{include}\:{p}\:\mathrm{as}\:\mathrm{a}\:\mathrm{factor}. \\ $$$$\mathrm{Hence}\:{p}\mid\left({a}+{p}\right)^{{p}} −{a}^{{p}} \\ $$
