Question Number 123600 by aurpeyz last updated on 26/Nov/20
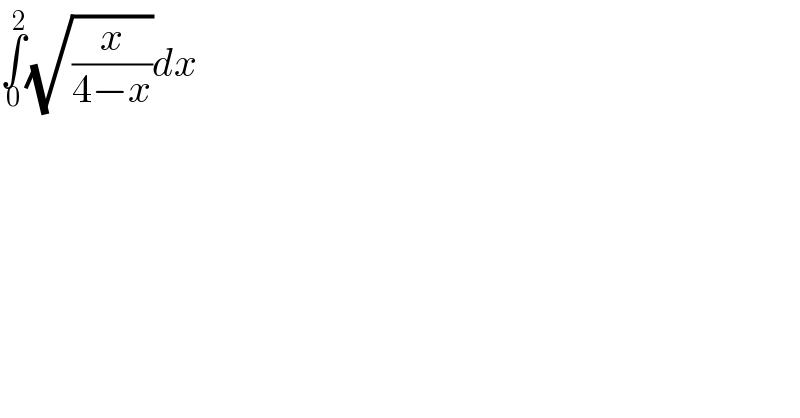
$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\sqrt{\frac{{x}}{\mathrm{4}−{x}}}{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Nov/20
![∫_0 ^2 (√(x/(4−x))) dx =∫_0 ^2 (√((2−x)/(2+x))) dx =∫_0 ^2 ((2−x)/( (√(4−x^2 ))))dx =∫_0 ^2 (2/( (√(4−x^2 ))))dx−∫_0 ^2 (x/( (√(4−x^2 ))))dx =2[sin^(−1) (x/2)]_0 ^2 +(1/2)∫_0 ^2 ((−2x)/( (√(4−x^2 ))))dx =π+[(√(4−x^2 ))]_0 ^2 =π−2](https://www.tinkutara.com/question/Q123605.png)
$$\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{{x}}{\mathrm{4}−{x}}}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}}\:{dx}\:\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx}−\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{2}\left[{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{−\mathrm{2}{x}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\pi+\left[\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{2}} =\pi−\mathrm{2} \\ $$
Commented by aurpeyz last updated on 26/Nov/20

$${pls}\:{explain}\:{line}\:\mathrm{2} \\ $$$$\frac{{x}}{\mathrm{4}−{x}}=\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}.\:{how}? \\ $$
Commented by Dwaipayan Shikari last updated on 26/Nov/20
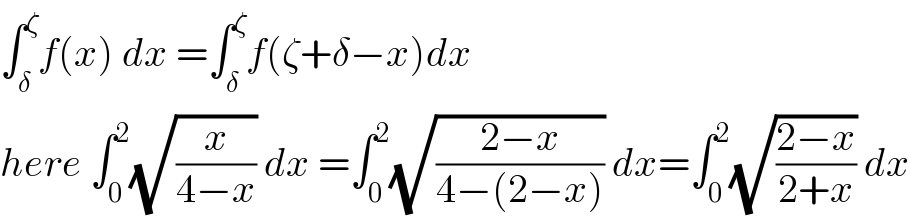
$$\int_{\delta} ^{\zeta} {f}\left({x}\right)\:{dx}\:=\int_{\delta} ^{\zeta} {f}\left(\zeta+\delta−{x}\right){dx} \\ $$$${here}\:\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{{x}}{\mathrm{4}−{x}}}\:{dx}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{\mathrm{2}−{x}}{\mathrm{4}−\left(\mathrm{2}−{x}\right)}}\:{dx}=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}}\:{dx} \\ $$
Commented by aurpeyz last updated on 26/Nov/20
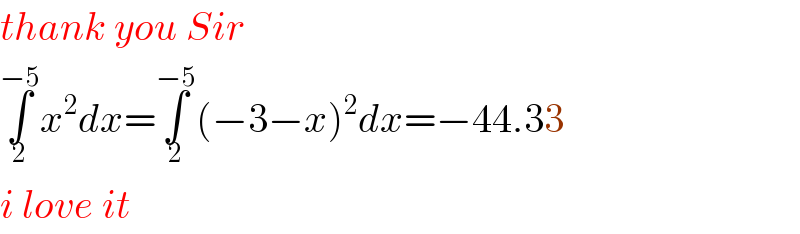
$${thank}\:{you}\:{Sir} \\ $$$$\underset{\mathrm{2}} {\overset{−\mathrm{5}} {\int}}{x}^{\mathrm{2}} {dx}=\underset{\mathrm{2}} {\overset{−\mathrm{5}} {\int}}\left(−\mathrm{3}−{x}\right)^{\mathrm{2}} {dx}=−\mathrm{44}.\mathrm{33}\: \\ $$$${i}\:{love}\:{it} \\ $$
Answered by mathmax by abdo last updated on 26/Nov/20
![I =∫_0 ^2 (√(x/(4−x)))dx changement x=4sin^2 t give ⇒sint=((√x)/2) I = ∫_0 ^(π/4) (√((4sin^2 t)/(4cos^2 t)))8sint cost dt =8 ∫_0 ^(π/4) ((sint)/(cost)).sint cost dt =8∫_0 ^(π/4) sin^2 t dt =4∫_0 ^(π/4) (1−cos(2t))dt =π−2[sin(2t)]_0 ^(π/4) =π−2 ⇒ I =π−2](https://www.tinkutara.com/question/Q123619.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{\mathrm{x}}{\mathrm{4}−\mathrm{x}}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{4sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{give}\:\:\Rightarrow\mathrm{sint}=\frac{\sqrt{\mathrm{x}}}{\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{4sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{4cos}^{\mathrm{2}} \mathrm{t}}}\mathrm{8sint}\:\mathrm{cost}\:\mathrm{dt} \\ $$$$=\mathrm{8}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{sint}}{\mathrm{cost}}.\mathrm{sint}\:\mathrm{cost}\:\mathrm{dt}\:=\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{dt}\:=\pi−\mathrm{2}\left[\mathrm{sin}\left(\mathrm{2t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\pi−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{I}\:=\pi−\mathrm{2} \\ $$
