Question Number 58091 by smiak8742 last updated on 17/Apr/19

$$\mathrm{27}{x}^{\mathrm{3}−\mathrm{1}=\mathrm{0}} \\ $$
Answered by MJS last updated on 17/Apr/19
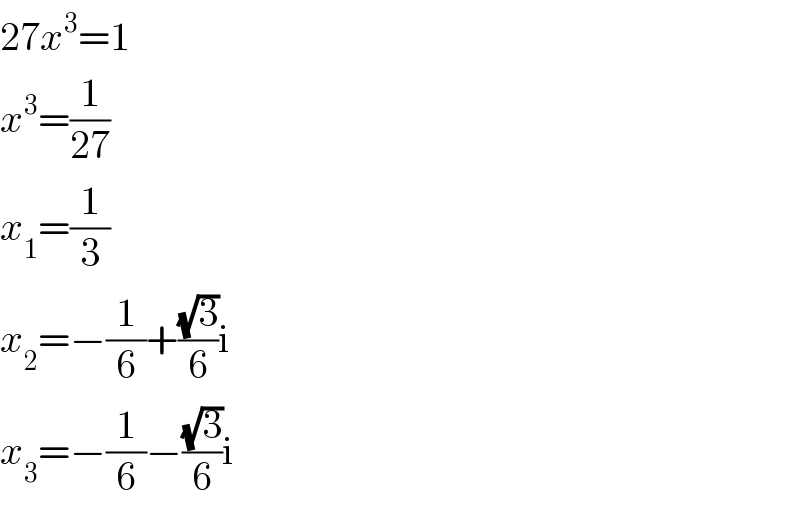
$$\mathrm{27}{x}^{\mathrm{3}} =\mathrm{1} \\ $$$${x}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{27}} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${x}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{i} \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{i} \\ $$
Commented by MJS last updated on 18/Apr/19
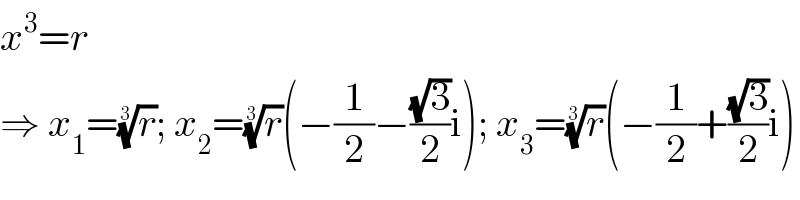
$${x}^{\mathrm{3}} ={r} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{{r}};\:{x}_{\mathrm{2}} =\sqrt[{\mathrm{3}}]{{r}}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right);\:{x}_{\mathrm{3}} =\sqrt[{\mathrm{3}}]{{r}}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right) \\ $$
Answered by Kunal12588 last updated on 17/Apr/19
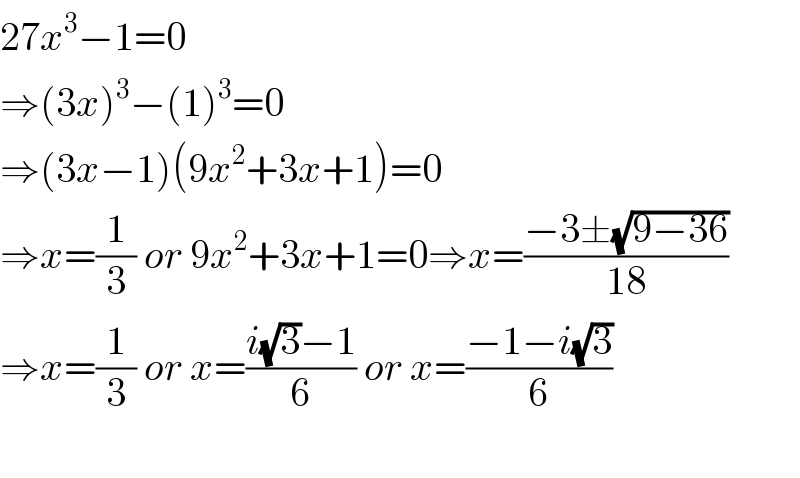
$$\mathrm{27}{x}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{3}{x}\right)^{\mathrm{3}} −\left(\mathrm{1}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{3}{x}−\mathrm{1}\right)\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}}\:{or}\:\mathrm{9}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{36}}}{\mathrm{18}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}}\:{or}\:{x}=\frac{{i}\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{6}}\:{or}\:{x}=\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$ \\ $$
