Question Number 123675 by mathmax by abdo last updated on 27/Nov/20
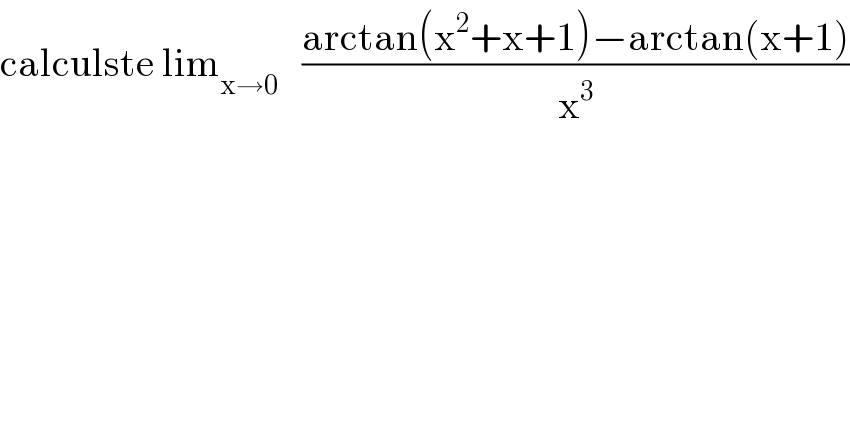
$$\mathrm{calculste}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)−\mathrm{arctan}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$
Answered by benjo_mathlover last updated on 27/Nov/20
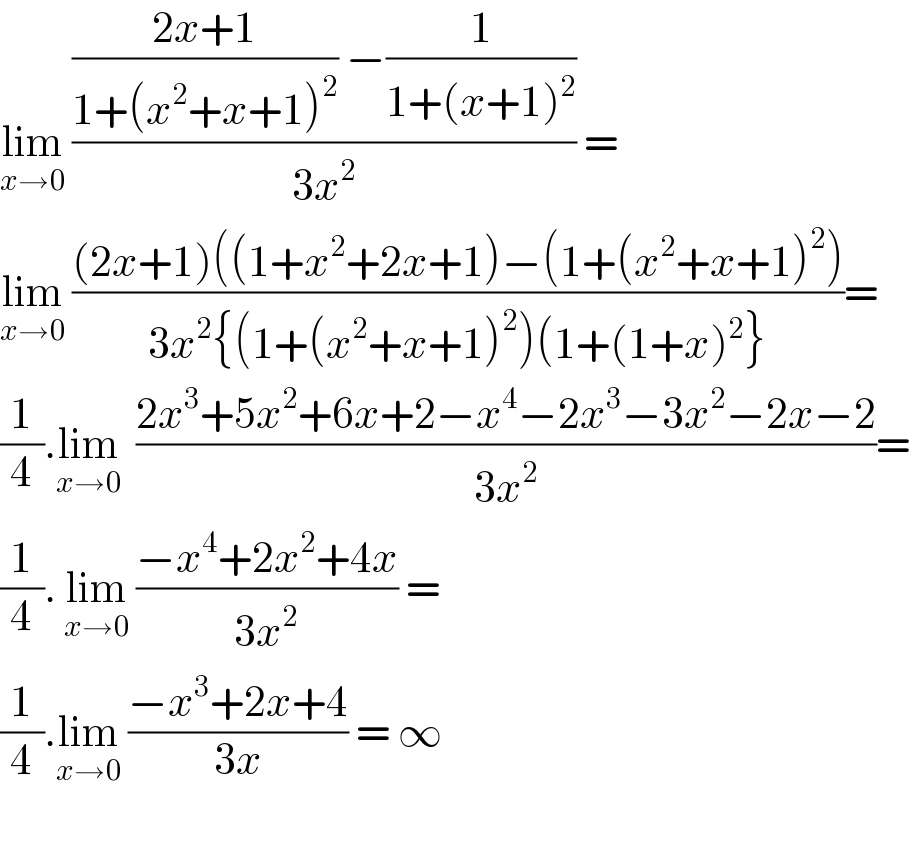
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{1}+\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{1}+\left({x}+\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{3}{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\left(\mathrm{1}+{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)−\left(\mathrm{1}+\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} \right)\right.}{\mathrm{3}{x}^{\mathrm{2}} \left\{\left(\mathrm{1}+\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} \right)\left(\mathrm{1}+\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \right\}\right.}= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}−{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}}{\mathrm{3}{x}^{\mathrm{2}} }\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{x}^{\mathrm{3}} +\mathrm{2}{x}+\mathrm{4}}{\mathrm{3}{x}}\:=\:\infty \\ $$$$ \\ $$
