Question Number 58196 by Umar last updated on 19/Apr/19

$$\mathrm{The}\:\mathrm{molar}\:\mathrm{heat}\:\mathrm{capacity}\:\mathrm{of}\:\mathrm{constant} \\ $$$$\mathrm{presure}\:\mathrm{of}\:\mathrm{a}\:\mathrm{gas}\:\mathrm{varies}\:\mathrm{with}\:\mathrm{the}\:\mathrm{temperature} \\ $$$$\mathrm{according}\:\mathrm{to}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{C}_{\mathrm{p}} \:=\:\:\mathrm{a}\:+\:\mathrm{b}\theta\:−\frac{\mathrm{C}}{\theta^{\mathrm{2}} } \\ $$$$\mathrm{where}\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{C}\:\mathrm{are}\:\mathrm{constants}. \\ $$$$\:\:\mathrm{How}\:\mathrm{much}\:\mathrm{heat}\:\mathrm{is}\:\mathrm{transfered}\:\mathrm{during} \\ $$$$\:\:\:\mathrm{an}\:\mathrm{isobaric}\:\mathrm{process}\:\mathrm{in}\:\mathrm{which}\:\mathrm{n}\:\mathrm{mole} \\ $$$$\:\:\:\mathrm{of}\:\mathrm{gas}\:\mathrm{undergo}\:\mathrm{a}\:\mathrm{temperature}\:\mathrm{rise} \\ $$$$\:\:\:\:\mathrm{from}\:\theta_{{i}\:} \mathrm{to}\:\theta_{{f}} \:? \\ $$
Answered by tanmay last updated on 19/Apr/19
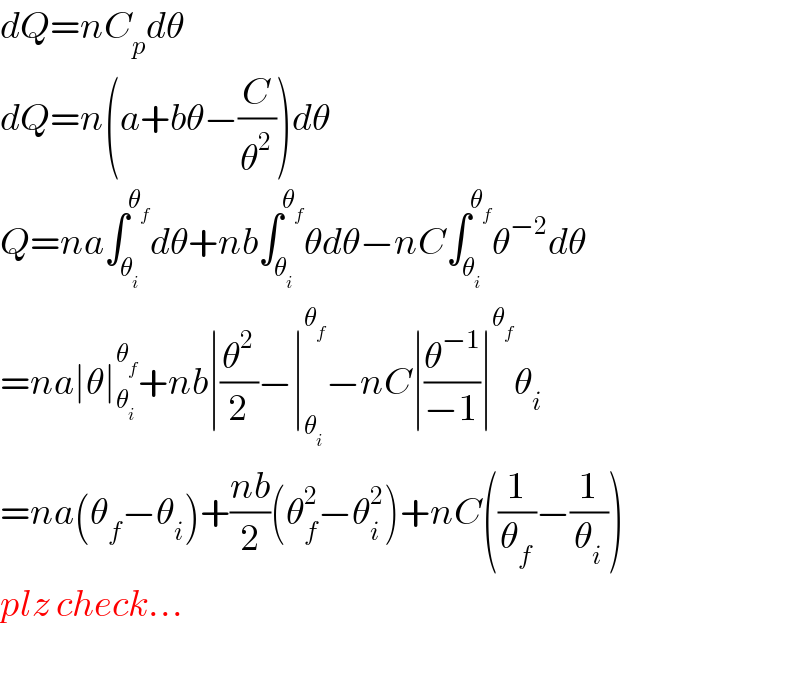
$${dQ}={nC}_{{p}} {d}\theta \\ $$$${dQ}={n}\left({a}+{b}\theta−\frac{{C}}{\theta^{\mathrm{2}} }\right){d}\theta \\ $$$${Q}={na}\int_{\theta_{{i}} } ^{\theta_{{f}} } {d}\theta+{nb}\int_{\theta_{{i}} } ^{\theta_{{f}} } \theta{d}\theta−{nC}\int_{\theta_{{i}} } ^{\theta_{{f}} } \theta^{−\mathrm{2}} {d}\theta \\ $$$$={na}\mid\theta\mid_{\theta_{{i}} } ^{\theta_{{f}} } +{nb}\mid\frac{\theta^{\mathrm{2}} }{\mathrm{2}}−\mid_{\theta_{{i}} } ^{\theta_{{f}} } −{nC}\mid\frac{\theta^{−\mathrm{1}} }{−\mathrm{1}}\mid^{\theta_{{f}} } \theta_{{i}} \\ $$$$={na}\left(\theta_{{f}} −\theta_{{i}} \right)+\frac{{nb}}{\mathrm{2}}\left(\theta_{{f}} ^{\mathrm{2}} −\theta_{{i}} ^{\mathrm{2}} \right)+{nC}\left(\frac{\mathrm{1}}{\theta_{{f}} }−\frac{\mathrm{1}}{\theta_{{i}} }\right) \\ $$$${plz}\:{check}… \\ $$$$ \\ $$
Commented by Umar last updated on 19/Apr/19

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{bunch} \\ $$
