Question Number 136813 by mnjuly1970 last updated on 26/Mar/21
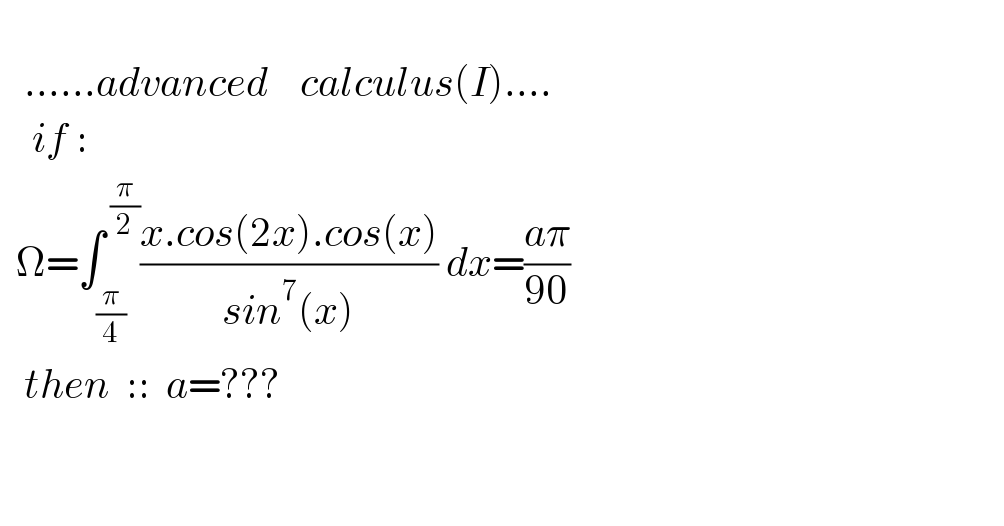
$$\:\:\:\:\: \\ $$$$\:\:\:……{advanced}\:\:\:\:{calculus}\left({I}\right)…. \\ $$$$\:\:\:\:{if}\::\: \\ $$$$\:\:\Omega=\int_{\frac{\pi}{\mathrm{4}}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{x}.{cos}\left(\mathrm{2}{x}\right).{cos}\left({x}\right)}{{sin}^{\mathrm{7}} \left({x}\right)}\:{dx}=\frac{{a}\pi}{\mathrm{90}} \\ $$$$\:\:\:{then}\:\:::\:\:{a}=??? \\ $$$$\:\: \\ $$$$\:\:\:\: \\ $$
Answered by Ar Brandon last updated on 26/Mar/21
![Ω=∫_(π/4) ^(π/2) ((xcos2xcosx)/(sin^7 x))dx=∫_(π/4) ^(π/2) ((x(1−2sin^2 x)cosx)/(sin^7 x))dx =∫_(π/4) ^(π/2) {x∙((cosx)/(sin^7 x))−x∙((2cosx)/(sin^5 x))}dx ={[x∙(1/(−6sin^6 x))+(1/6)∫(dx/(sin^6 x))]−2[x∙(1/(−4sin^4 x))+(1/4)∫(dx/(sin^4 x))]}_(π/4) ^(π/2) =−(π/2)∙(1/6)+(π/4)∙(8/6)+2((π/2)∙(1/4)−(π/4))+(1/6)∫_(π/4) ^(π/2) (dx/(sin^6 x))−(1/2)∫_(π/4) ^(π/2) (dx/(sin^4 x)) =(1/6)∫_(π/4) ^(π/2) (dx/(sin^6 x))−(1/2)∫_(π/4) ^(π/2) (dx/(sin^4 x)) =(1/6)∫_(π/4) ^(π/2) cosec^2 x(1+cot^2 x)^2 dx−(1/2)∫_(π/4) ^(π/2) (cosec^2 x)(cot^2 x+1)dx =[(1/2)(((cot^3 x)/3)+cotx)−(1/6)(cotx+2((cot^3 x)/3)+((cot^5 x)/5))]_(π/4) ^(π/2) =−((16)/(45))=((aπ)/(90)) , a=−((32)/π)](https://www.tinkutara.com/question/Q136818.png)
$$\Omega=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{xcos2xcosx}}{\mathrm{sin}^{\mathrm{7}} \mathrm{x}}\mathrm{dx}=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{x}\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{cosx}}{\mathrm{sin}^{\mathrm{7}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\:\:\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \left\{\mathrm{x}\centerdot\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{7}} \mathrm{x}}−\mathrm{x}\centerdot\frac{\mathrm{2cosx}}{\mathrm{sin}^{\mathrm{5}} \mathrm{x}}\right\}\mathrm{dx} \\ $$$$\:\:\:\:=\left\{\left[\mathrm{x}\centerdot\frac{\mathrm{1}}{−\mathrm{6sin}^{\mathrm{6}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{6}} \mathrm{x}}\right]−\mathrm{2}\left[\mathrm{x}\centerdot\frac{\mathrm{1}}{−\mathrm{4sin}^{\mathrm{4}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{4}} \mathrm{x}}\right]\right\}_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\:\:=−\frac{\pi}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{6}}+\frac{\pi}{\mathrm{4}}\centerdot\frac{\mathrm{8}}{\mathrm{6}}+\mathrm{2}\left(\frac{\pi}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{4}}−\frac{\pi}{\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{6}} \mathrm{x}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{4}} \mathrm{x}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{6}} \mathrm{x}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{4}} \mathrm{x}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cosec}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} \mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cosec}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{cot}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)\mathrm{dx} \\ $$$$\:\:\:\:=\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{cot}^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}+\mathrm{cotx}\right)−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{cotx}+\mathrm{2}\frac{\mathrm{cot}^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}+\frac{\mathrm{cot}^{\mathrm{5}} \mathrm{x}}{\mathrm{5}}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} =−\frac{\mathrm{16}}{\mathrm{45}}=\frac{\mathrm{a}\pi}{\mathrm{90}}\:,\:\mathrm{a}=−\frac{\mathrm{32}}{\pi} \\ $$
Commented by mnjuly1970 last updated on 26/Mar/21

$$\:\:\:{thanks}\:\:{alot}\:… \\ $$
Commented by Ar Brandon last updated on 26/Mar/21
You're welcome Sir !
