Question Number 58313 by mr W last updated on 21/Apr/19
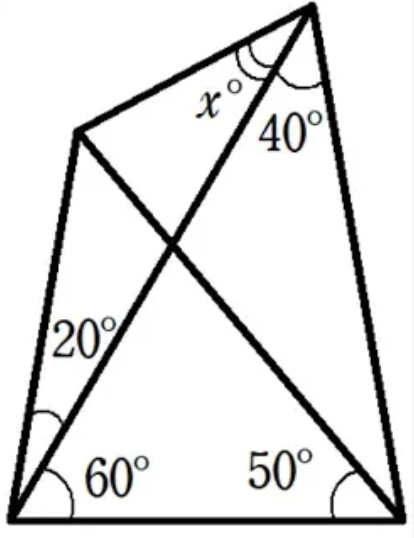
Commented by tanmay last updated on 21/Apr/19
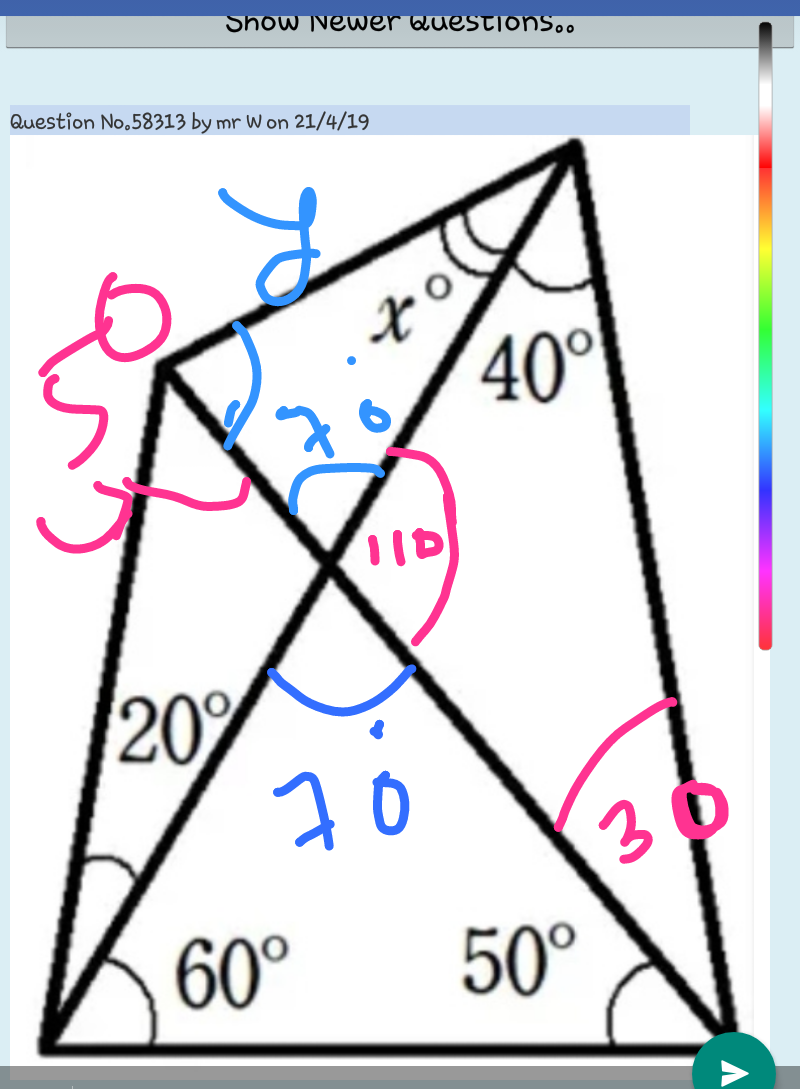
Commented by tanmay last updated on 21/Apr/19
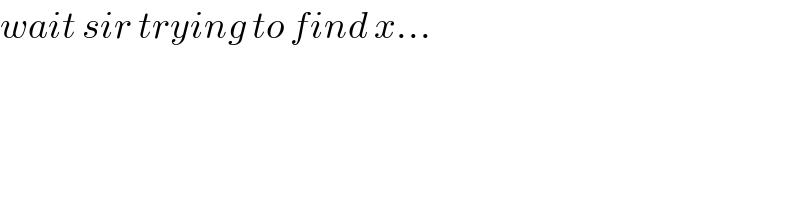
$${wait}\:{sir}\:{trying}\:{to}\:{find}\:{x}… \\ $$
Answered by mr W last updated on 21/Apr/19
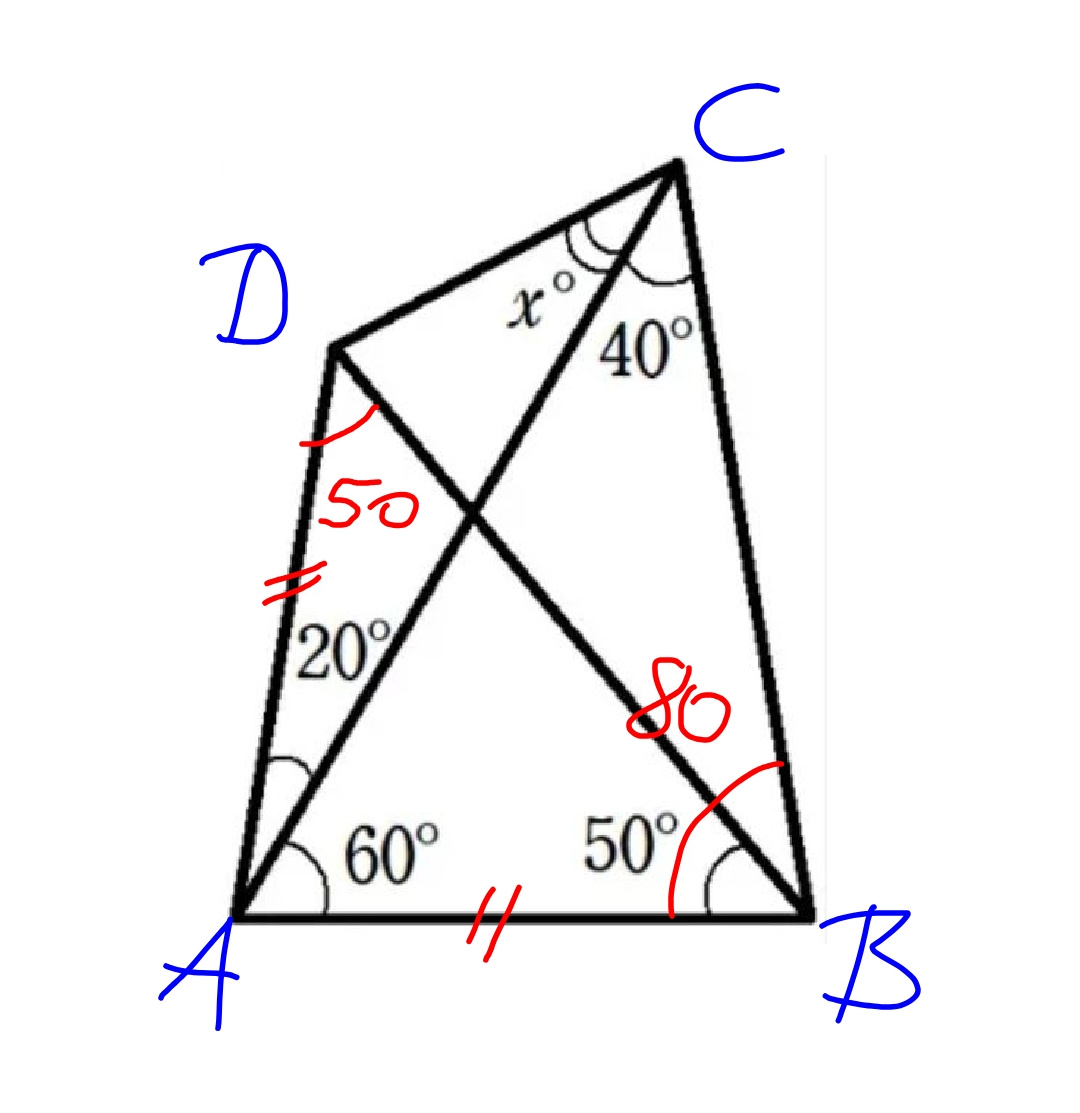
Commented by mr W last updated on 21/Apr/19

$${Method}\:\mathrm{1}\:{using}\:{trigonometry}: \\ $$$$\frac{{AC}}{{AD}}=\frac{\mathrm{sin}\:\left({x}+\mathrm{20}\right)}{\mathrm{sin}\:{x}} \\ $$$$\frac{{AC}}{{AB}}=\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{40}} \\ $$$${since}\:{AB}={AD}, \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left({x}+\mathrm{20}\right)}{\mathrm{sin}\:{x}}=\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{40}}=\mathrm{2}\:\mathrm{cos}\:\mathrm{40}=\mathrm{2}\:\mathrm{sin}\:\mathrm{50}=\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{30}+\mathrm{20}\right)=\mathrm{cos}\:\mathrm{20}+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{20} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{20}+\frac{\mathrm{sin}\:\mathrm{20}}{\mathrm{tan}\:{x}}=\mathrm{cos}\:\mathrm{20}+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{20} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}=\mathrm{30}° \\ $$
Answered by mr W last updated on 21/Apr/19
Commented by mr W last updated on 21/Apr/19
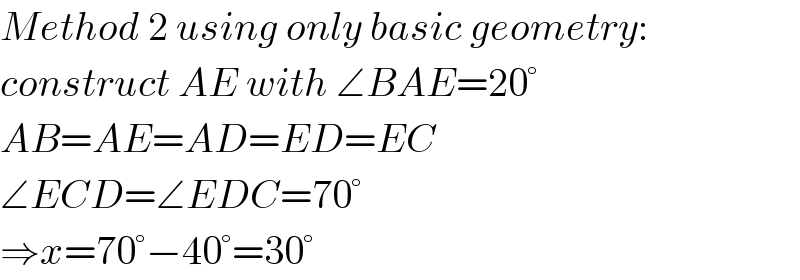
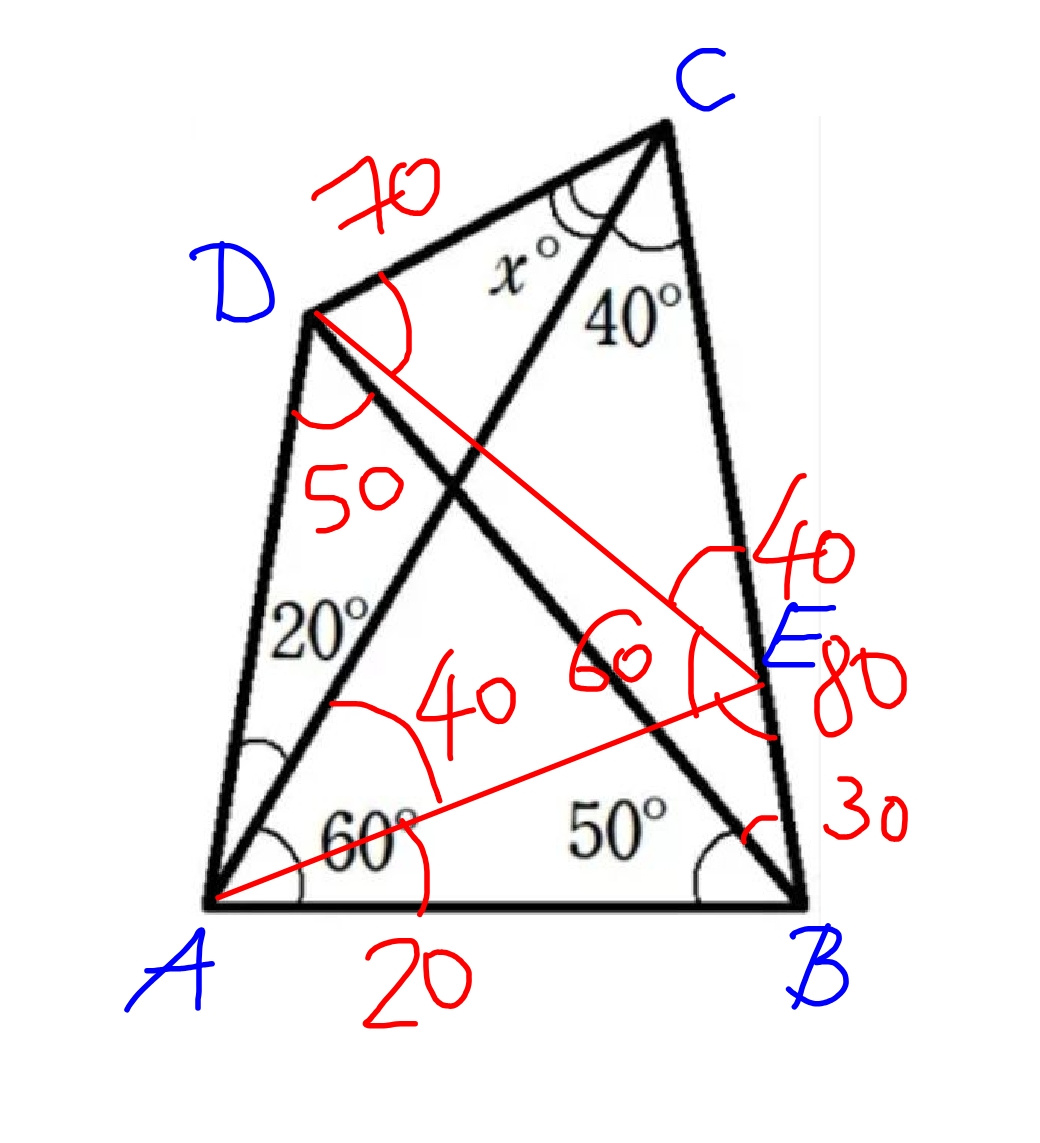
$${Method}\:\mathrm{2}\:{using}\:{only}\:{basic}\:{geometry}: \\ $$$${construct}\:{AE}\:{with}\:\angle{BAE}=\mathrm{20}° \\ $$$${AB}={AE}={AD}={ED}={EC} \\ $$$$\angle{ECD}=\angle{EDC}=\mathrm{70}° \\ $$$$\Rightarrow{x}=\mathrm{70}°−\mathrm{40}°=\mathrm{30}° \\ $$
Commented by tanmay last updated on 21/Apr/19

$${thsnk}\:{yousir}… \\ $$
Commented by salahahmed last updated on 22/Apr/19
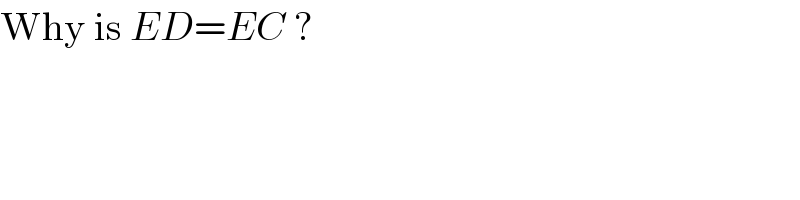
$$\mathrm{Why}\:\mathrm{is}\:{ED}={EC}\:? \\ $$
Commented by mr W last updated on 22/Apr/19

$$\angle{CAE}=\angle{ACE}=\mathrm{40}° \\ $$$$\Rightarrow{EC}={EA}={ED} \\ $$
Commented by salahahmed last updated on 23/Apr/19
Thank you sir
