Question Number 189418 by TUN last updated on 16/Mar/23
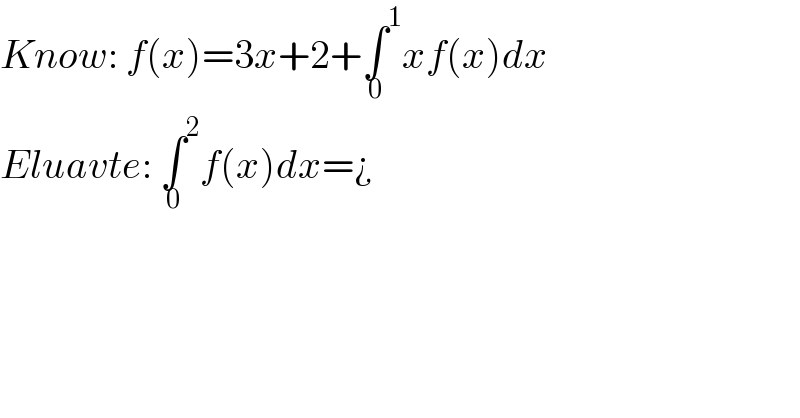
$${Know}:\:{f}\left({x}\right)=\mathrm{3}{x}+\mathrm{2}+\underset{\mathrm{0}} {\int}^{\mathrm{1}} {xf}\left({x}\right){dx} \\ $$$${Eluavte}:\:\underset{\mathrm{0}} {\int}^{\mathrm{2}} {f}\left({x}\right){dx}=¿ \\ $$
Answered by mr W last updated on 16/Mar/23
![say ∫_0 ^1 xf(x)dx=A=constant f(x)=3x+2+A ∫_0 ^1 xf(x)=∫_0 ^1 [3x^2 +(2+A)x]dx=1^3 +(((2+A)1^2 )/2)=2+(A/2) 2+(A/2)=A ⇒A=4 ⇒f(x)=3x+2+4=3x+6 ∫_0 ^2 f(x)dx=∫_0 ^2 (3x+6)dx=((3×2^2 )/2)+6×2=18](https://www.tinkutara.com/question/Q189420.png)
$${say}\:\int_{\mathrm{0}} ^{\mathrm{1}} {xf}\left({x}\right){dx}={A}={constant} \\ $$$${f}\left({x}\right)=\mathrm{3}{x}+\mathrm{2}+{A} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {xf}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \left[\mathrm{3}{x}^{\mathrm{2}} +\left(\mathrm{2}+{A}\right){x}\right]{dx}=\mathrm{1}^{\mathrm{3}} +\frac{\left(\mathrm{2}+{A}\right)\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2}+\frac{{A}}{\mathrm{2}} \\ $$$$\mathrm{2}+\frac{{A}}{\mathrm{2}}={A} \\ $$$$\Rightarrow{A}=\mathrm{4} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{3}{x}+\mathrm{2}+\mathrm{4}=\mathrm{3}{x}+\mathrm{6} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{3}{x}+\mathrm{6}\right){dx}=\frac{\mathrm{3}×\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{6}×\mathrm{2}=\mathrm{18} \\ $$
