Menu Close

A-n-1-5-n-1-5-n-A-n-

Tinku Tara 0 Comments
Pin




Question Number 124041 by pticantor last updated on 30/Nov/20
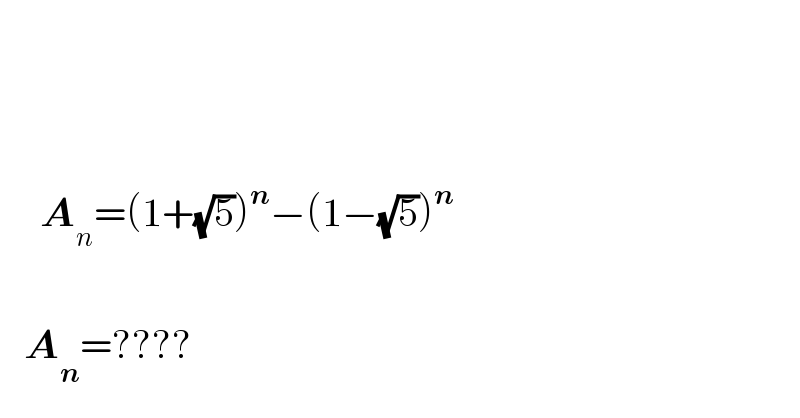
A_n =(1+(√5))^n −(1−(√5))^n A_n =????
$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\boldsymbol{{A}}_{{n}} =\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\boldsymbol{{n}}} −\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{\boldsymbol{{n}}} \\ $$$$ \\ $$$$\:\:\:\boldsymbol{{A}}_{\boldsymbol{{n}}} =???? \\ $$
Commented by Dwaipayan Shikari last updated on 30/Nov/20
A_n =(1+(√5))^n −(1−(√5))^n (A_n /( 2^n (√5)))=(1/( (√5)))((((1+(√5))/2))^n −(((1−(√5))/2))^n ) ⇒(A_n /(2^n (√5)))=F_n ⇒A_n =2^n (√5) F_n (F_n =nth Fibbonocci Number) Fibbonocci sequence 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2594,4191,6785.... A_n sequence 2(√5), 4(√5), 16(√5) , 48(√5) , 160(√5), 512(√5) , 832(√5), 2688(√5) ,8704(√5),...
$${A}_{{n}} =\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{{n}} −\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{{n}} \\ $$$$\frac{{A}_{{n}} }{\:\mathrm{2}^{{n}} \sqrt{\mathrm{5}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \right) \\ $$$$\Rightarrow\frac{{A}_{{n}} }{\mathrm{2}^{{n}} \sqrt{\mathrm{5}}}={F}_{{n}} \:\:\:\:\:\:\:\:\:\:\:\Rightarrow{A}_{{n}} =\mathrm{2}^{{n}} \sqrt{\mathrm{5}}\:{F}_{{n}} \:\:\:\:\:\:\:\left({F}_{{n}} ={nth}\:{Fibbonocci}\:{Number}\right) \\ $$$${Fibbonocci}\:{sequence} \\ $$$$\mathrm{1},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{8},\mathrm{13},\mathrm{21},\mathrm{34},\mathrm{55},\mathrm{89},\mathrm{144},\mathrm{233},\mathrm{377},\mathrm{610},\mathrm{987},\mathrm{1597},\mathrm{2594},\mathrm{4191},\mathrm{6785}…. \\ $$$${A}_{{n}} \:{sequence} \\ $$$$\mathrm{2}\sqrt{\mathrm{5}},\:\mathrm{4}\sqrt{\mathrm{5}},\:\mathrm{16}\sqrt{\mathrm{5}}\:,\:\mathrm{48}\sqrt{\mathrm{5}}\:,\:\mathrm{160}\sqrt{\mathrm{5}},\:\mathrm{512}\sqrt{\mathrm{5}}\:,\:\mathrm{832}\sqrt{\mathrm{5}},\:\mathrm{2688}\sqrt{\mathrm{5}}\:,\mathrm{8704}\sqrt{\mathrm{5}},… \\ $$
Answered by Bird last updated on 30/Nov/20
A_n =Σ_(k=0) ^n C_n ^k ((√5))^k −Σ_(k=0) ^n C_n ^k (−1)^k ((√5))^k =Σ_(k=0) ^n C_n ^k {1−(−1)^k }((√5))^k =2Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) ((√5))^(2p+1) =2(√5) Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) 5^p
$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(\sqrt{\mathrm{5}}\right)^{{k}} −\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \left(\sqrt{\mathrm{5}}\right)^{{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \left\{\mathrm{1}−\left(−\mathrm{1}\right)^{{k}} \right\}\left(\sqrt{\mathrm{5}}\right)^{{k}} \\ $$$$=\mathrm{2}\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:\:\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}{p}+\mathrm{1}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{5}}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\mathrm{5}^{{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *