Question Number 124046 by john_santu last updated on 30/Nov/20
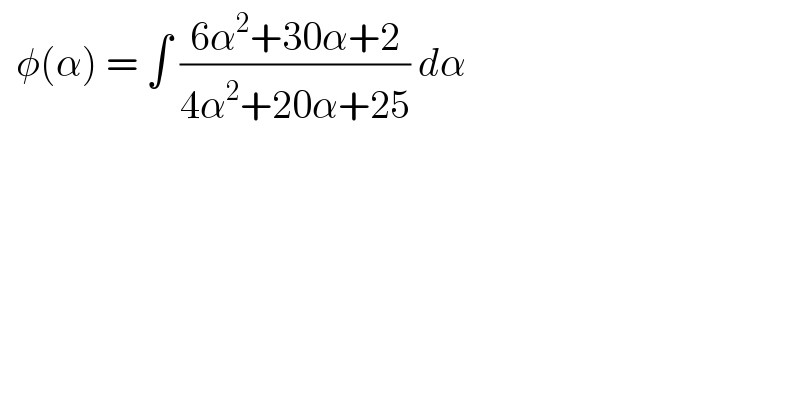
$$\:\:\phi\left(\alpha\right)\:=\:\int\:\frac{\mathrm{6}\alpha^{\mathrm{2}} +\mathrm{30}\alpha+\mathrm{2}}{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{20}\alpha+\mathrm{25}}\:{d}\alpha\: \\ $$
Answered by liberty last updated on 30/Nov/20
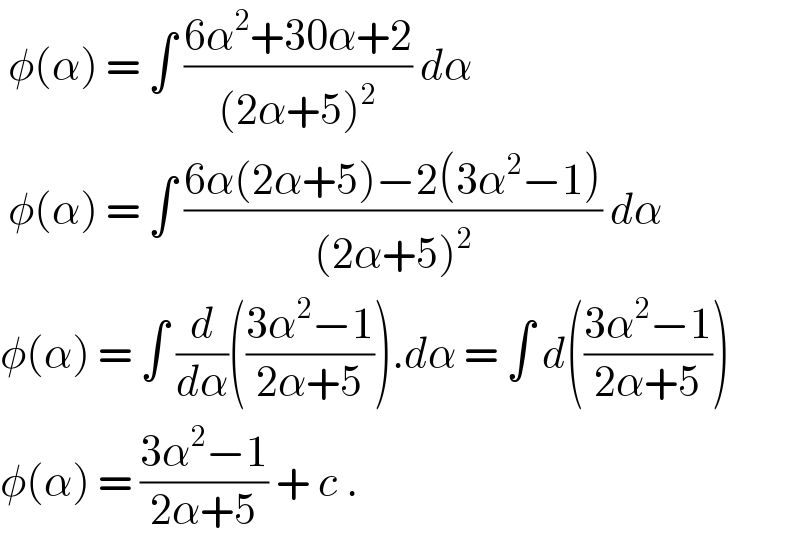
$$\:\phi\left(\alpha\right)\:=\:\int\:\frac{\mathrm{6}\alpha^{\mathrm{2}} +\mathrm{30}\alpha+\mathrm{2}}{\left(\mathrm{2}\alpha+\mathrm{5}\right)^{\mathrm{2}} }\:{d}\alpha \\ $$$$\:\phi\left(\alpha\right)\:=\:\int\:\frac{\mathrm{6}\alpha\left(\mathrm{2}\alpha+\mathrm{5}\right)−\mathrm{2}\left(\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{2}\alpha+\mathrm{5}\right)^{\mathrm{2}} }\:{d}\alpha \\ $$$$\phi\left(\alpha\right)\:=\:\int\:\frac{{d}}{{d}\alpha}\left(\frac{\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\alpha+\mathrm{5}}\right).{d}\alpha\:=\:\int\:{d}\left(\frac{\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\alpha+\mathrm{5}}\right) \\ $$$$\phi\left(\alpha\right)\:=\:\frac{\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\alpha+\mathrm{5}}\:+\:{c}\:. \\ $$
