Menu Close

intregation-collected-problem-

Tinku Tara 0 Comments
Pin




Question Number 124076 by TANMAY PANACEA last updated on 30/Nov/20
intregation...collected problem
$${intregation}…{collected}\:{problem} \\ $$
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
calculus collected roblem
$$\boldsymbol{{calculus}}\:\boldsymbol{{collected}}\:\boldsymbol{{roblem}} \\ $$
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
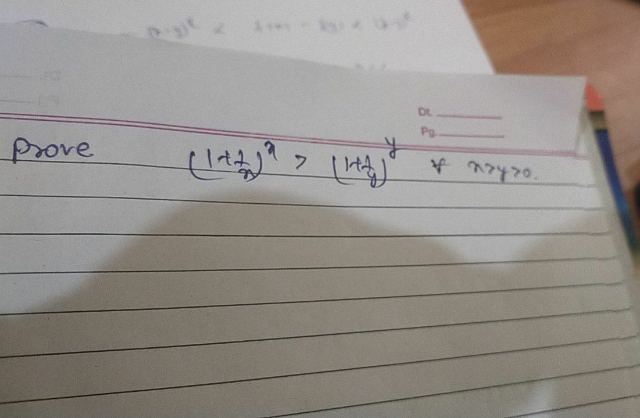
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by Dwaipayan Shikari last updated on 30/Nov/20
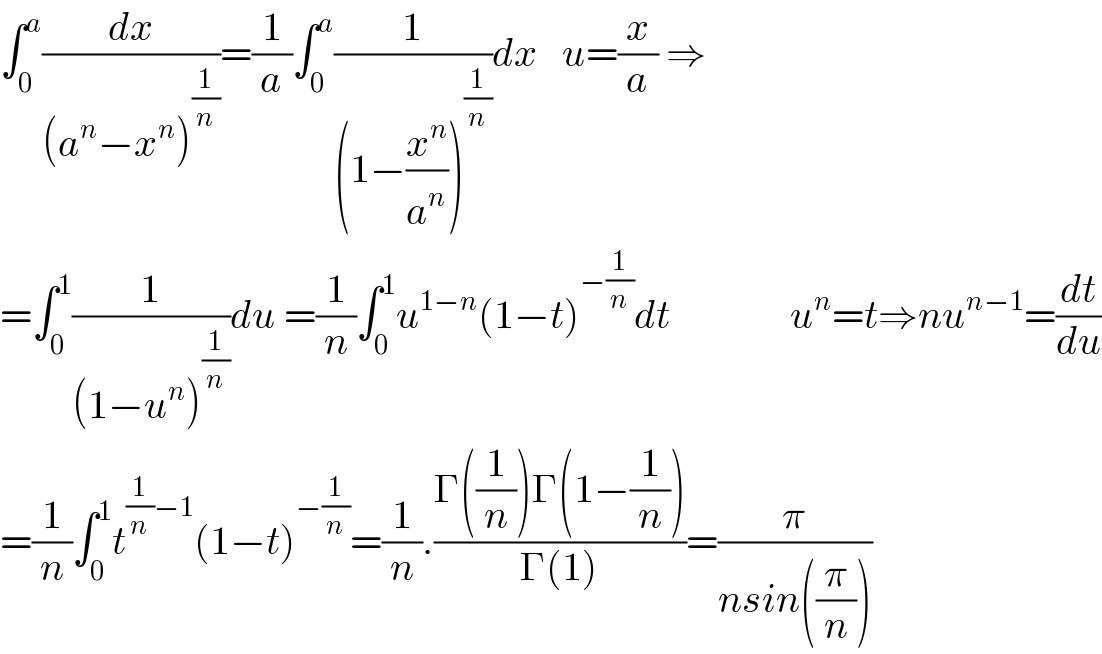
∫_0 ^a (dx/((a^n −x^n )^(1/n) ))=(1/a)∫_0 ^a (1/((1−(x^n /a^n ))^(1/n) ))dx u=(x/a) ⇒ =∫_0 ^1 (1/((1−u^n )^(1/n) ))du =(1/n)∫_0 ^1 u^(1−n) (1−t)^(−(1/n)) dt u^n =t⇒nu^(n−1) =(dt/du) =(1/n)∫_0 ^1 t^((1/n)−1) (1−t)^(−(1/n)) =(1/n).((Γ((1/n))Γ(1−(1/n)))/(Γ(1)))=(π/(nsin((π/n))))
$$\int_{\mathrm{0}} ^{{a}} \frac{{dx}}{\left({a}^{{n}} −{x}^{{n}} \right)^{\frac{\mathrm{1}}{{n}}} }=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{{a}} \frac{\mathrm{1}}{\left(\mathrm{1}−\frac{{x}^{{n}} }{{a}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} }{dx}\:\:\:{u}=\frac{{x}}{{a}}\:\Rightarrow \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}−{u}^{{n}} \right)^{\frac{\mathrm{1}}{{n}}} }{du}\:=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{1}−{n}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{{n}}} {dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}^{{n}} ={t}\Rightarrow{nu}^{{n}−\mathrm{1}} =\frac{{dt}}{{du}} \\ $$$$=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{{n}}} =\frac{\mathrm{1}}{{n}}.\frac{\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\pi}{{nsin}\left(\frac{\pi}{{n}}\right)}\: \\ $$
Commented by TANMAY PANACEA last updated on 30/Nov/20
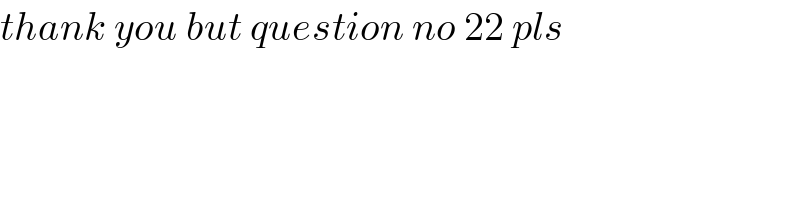
thank you but question no 22 pls
$${thank}\:{you}\:{but}\:{question}\:{no}\:\mathrm{22}\:{pls} \\ $$
Commented by mnjuly1970 last updated on 30/Nov/20
note:: Γ(x)Γ(1−x)=(π/(sin(πx))) note:: ∫_0 ^( π) ln(sin(x))dx=−πln(2) Ω=∫_0 ^( 1) ln(Γ(x))dx Ω=∫_0 ^( 1) ln(Γ(1−x))dx 2Ω=∫_0 ^( 1) ln[(Γ(x)Γ(1−x))]dx 2Ω =^(euler reflection formula) ∫_0 ^( 1) ln((π/(sin(πx))))dx =ln(π)−∫_0 ^( 1) ln(sin(πx))dx =^(πx=t) ln(π)−(1/π)∫_0 ^( π) ln(sin(x))dx =ln(π)−(1/π)(−πln(2)) =ln(π)+ln(2)=ln(2π) ∴ Ω=(1/2)ln(2π)=ln((√(2π)) )✓
$$\:\:\:\:{note}::\:\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)=\frac{\pi}{{sin}\left(\pi{x}\right)} \\ $$$$\:{note}::\:\:\int_{\mathrm{0}} ^{\:\pi} {ln}\left({sin}\left({x}\right)\right){dx}=−\pi{ln}\left(\mathrm{2}\right) \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\Gamma\left({x}\right)\right){dx} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\Gamma\left(\mathrm{1}−{x}\right)\right){dx} \\ $$$$\:\mathrm{2}\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left[\left(\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)\right)\right]{dx} \\ $$$$\:\:\mathrm{2}\Omega\:\overset{{euler}\:{reflection}\:{formula}} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\frac{\pi}{{sin}\left(\pi{x}\right)}\right){dx} \\ $$$$={ln}\left(\pi\right)−\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({sin}\left(\pi{x}\right)\right){dx} \\ $$$$\overset{\pi{x}={t}} {=}{ln}\left(\pi\right)−\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\:\pi} {ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$={ln}\left(\pi\right)−\frac{\mathrm{1}}{\pi}\left(−\pi{ln}\left(\mathrm{2}\right)\right) \\ $$$$={ln}\left(\pi\right)+{ln}\left(\mathrm{2}\right)={ln}\left(\mathrm{2}\pi\right) \\ $$$$\therefore\:\:\Omega=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi\right)={ln}\left(\sqrt{\mathrm{2}\pi}\:\right)\checkmark \\ $$
Commented by TANMAY PANACEA last updated on 30/Nov/20
excellent
$${excellent} \\ $$
Commented by mnjuly1970 last updated on 30/Nov/20
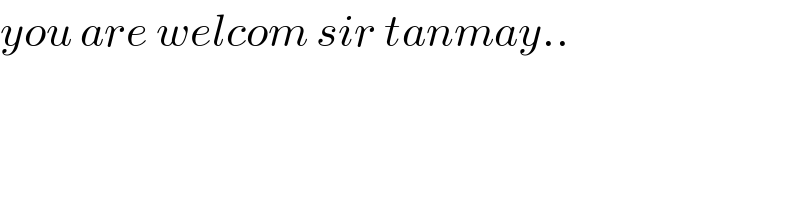
you are welcom sir tanmay..
$${you}\:{are}\:{welcom}\:{sir}\:{tanmay}.. \\ $$
Commented by Dwaipayan Shikari last updated on 30/Nov/20
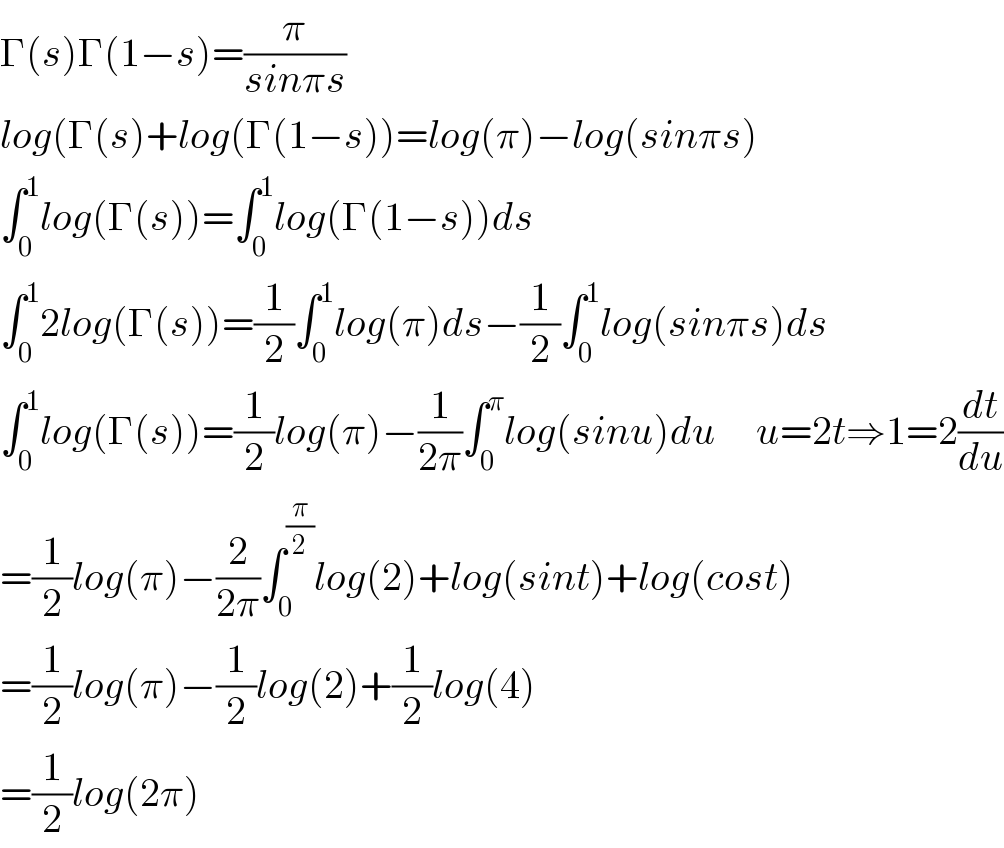
Γ(s)Γ(1−s)=(π/(sinπs)) log(Γ(s)+log(Γ(1−s))=log(π)−log(sinπs) ∫_0 ^1 log(Γ(s))=∫_0 ^1 log(Γ(1−s))ds ∫_0 ^1 2log(Γ(s))=(1/2)∫_0 ^1 log(π)ds−(1/2)∫_0 ^1 log(sinπs)ds ∫_0 ^1 log(Γ(s))=(1/2)log(π)−(1/(2π))∫_0 ^π log(sinu)du u=2t⇒1=2(dt/du) =(1/2)log(π)−(2/(2π))∫_0 ^(π/2) log(2)+log(sint)+log(cost) =(1/2)log(π)−(1/2)log(2)+(1/2)log(4) =(1/2)log(2π)
$$\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\frac{\pi}{{sin}\pi{s}} \\ $$$${log}\left(\Gamma\left({s}\right)+{log}\left(\Gamma\left(\mathrm{1}−{s}\right)\right)={log}\left(\pi\right)−{log}\left({sin}\pi{s}\right)\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left({s}\right)\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left(\mathrm{1}−{s}\right)\right){ds} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{log}\left(\Gamma\left({s}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\pi\right){ds}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({sin}\pi{s}\right){ds} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left({s}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\pi\right)−\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\pi} {log}\left({sinu}\right){du}\:\:\:\:\:{u}=\mathrm{2}{t}\Rightarrow\mathrm{1}=\mathrm{2}\frac{{dt}}{{du}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\pi\right)−\frac{\mathrm{2}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{2}\right)+{log}\left({sint}\right)+{log}\left({cost}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\pi\right)−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{4}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\pi\right) \\ $$
Commented by Dwaipayan Shikari last updated on 30/Nov/20
∫_0 ^(π/2) (1/( (√(acos^4 x+bsin^4 x))))dx =∫_0 ^(π/2) ((sec^2 x)/( (√(a+btan^4 x))))dx=∫_0 ^∞ (dt/( (√(a+bt^4 )))) a+bt^4 =u^2 ⇒2bt^3 =u(du/dt) =(1/2)∫_(√a) ^∞ ((udu)/(ubt^3 ))=(1/(2b))∫_(√a) ^∞ (du/((((u^2 −a)/b))^(3/4) )) =(1/(2 (b)^(1/4) ))∫_0 ^∞ (du/((u^2 −a)^(3/4) )) u^2 −a=p⇒2u=(dp/du) =(1/(4(b)^(1/4) ))∫_0 ^∞ (dp/(p^(3/4) (a+p)^(1/2) ))=(1/(4((ab))^(1/4) ))∫_0 ^∞ (1/(Φ^(3/4) (1+Φ)^(1/2) ))dΦ Φ=(p/a) =(1/(4((ab))^(1/4) ))∫_0 ^1 Λ^(−(3/4)) (1−Λ)^(−(3/4)) dΛ (Φ/(1+Φ))=Λ =(1/(4((ab))^(1/4) )).Γ^2 ((1/4)).(1/(Γ((1/2))))=((Γ^2 ((1/4)))/(4((π^2 ab))^(1/4) ))
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{{acos}^{\mathrm{4}} {x}+{bsin}^{\mathrm{4}} {x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} {x}}{\:\sqrt{{a}+{btan}^{\mathrm{4}} {x}}}{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\:\sqrt{{a}+{bt}^{\mathrm{4}} }}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}+{bt}^{\mathrm{4}} ={u}^{\mathrm{2}} \Rightarrow\mathrm{2}{bt}^{\mathrm{3}} ={u}\frac{{du}}{{dt}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{{a}}} ^{\infty} \frac{{udu}}{{ubt}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}{b}}\int_{\sqrt{{a}}} ^{\infty} \frac{{du}}{\left(\frac{{u}^{\mathrm{2}} −{a}}{{b}}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\:\sqrt[{\mathrm{4}}]{{b}}}\int_{\mathrm{0}} ^{\infty} \frac{{du}}{\left({u}^{\mathrm{2}} −{a}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}^{\mathrm{2}} −{a}={p}\Rightarrow\mathrm{2}{u}=\frac{{dp}}{{du}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt[{\mathrm{4}}]{{b}}}\int_{\mathrm{0}} ^{\infty} \frac{{dp}}{{p}^{\frac{\mathrm{3}}{\mathrm{4}}} \left({a}+{p}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{1}}{\mathrm{4}\sqrt[{\mathrm{4}}]{{ab}}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\Phi^{\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}+\Phi\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{d}\Phi\:\:\:\:\:\:\Phi=\frac{{p}}{{a}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt[{\mathrm{4}}]{{ab}}}\int_{\mathrm{0}} ^{\mathrm{1}} \Lambda^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−\Lambda\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} {d}\Lambda\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\Phi}{\mathrm{1}+\Phi}=\Lambda \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt[{\mathrm{4}}]{{ab}}}.\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right).\frac{\mathrm{1}}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt[{\mathrm{4}}]{\pi^{\mathrm{2}} {ab}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *