Question Number 124151 by mohammad17 last updated on 01/Dec/20
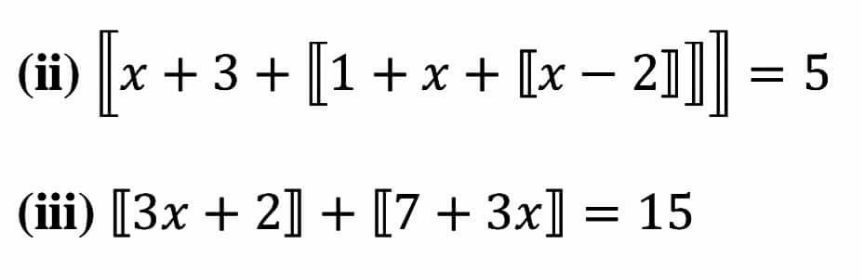
Answered by MJS_new last updated on 01/Dec/20
![[ax+b]=[ax]+b (ii) [x+3+[1+x+[x−2]]]= =[x+3+[1+x+[x]−2]]= =[x+3+[x+[x]−1]]= =[x+3+[x]+[x]−1]= =[x+2[x]+2]= =3[x]+2 3[x]+2=5 ⇒ [x]=1 ⇒ 1≤x<2 (iii) [3x+2]+[3x+7]=15 2[3x]+9=15 [3x]=3 ⇒ 3≤3x<4 ⇒ 1≤x<(4/3)](https://www.tinkutara.com/question/Q124155.png)
$$\left[{ax}+{b}\right]=\left[{ax}\right]+{b} \\ $$$$\left(\mathrm{ii}\right)\:\left[{x}+\mathrm{3}+\left[\mathrm{1}+{x}+\left[{x}−\mathrm{2}\right]\right]\right]= \\ $$$$\:\:\:\:\:\:\:\:=\left[{x}+\mathrm{3}+\left[\mathrm{1}+{x}+\left[{x}\right]−\mathrm{2}\right]\right]= \\ $$$$\:\:\:\:\:\:\:\:=\left[{x}+\mathrm{3}+\left[{x}+\left[{x}\right]−\mathrm{1}\right]\right]= \\ $$$$\:\:\:\:\:\:\:\:=\left[{x}+\mathrm{3}+\left[{x}\right]+\left[{x}\right]−\mathrm{1}\right]= \\ $$$$\:\:\:\:\:\:\:\:=\left[{x}+\mathrm{2}\left[{x}\right]+\mathrm{2}\right]= \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{3}\left[{x}\right]+\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{3}\left[{x}\right]+\mathrm{2}=\mathrm{5}\:\Rightarrow\:\left[{x}\right]=\mathrm{1}\:\Rightarrow\:\mathrm{1}\leqslant{x}<\mathrm{2} \\ $$$$\left(\mathrm{iii}\right)\:\left[\mathrm{3}{x}+\mathrm{2}\right]+\left[\mathrm{3}{x}+\mathrm{7}\right]=\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2}\left[\mathrm{3}{x}\right]+\mathrm{9}=\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{3}{x}\right]=\mathrm{3}\:\Rightarrow\:\mathrm{3}\leqslant\mathrm{3}{x}<\mathrm{4}\:\Rightarrow\:\mathrm{1}\leqslant{x}<\frac{\mathrm{4}}{\mathrm{3}} \\ $$
