Question-124347

Question Number 124347 by Dwaipayan Shikari last updated on 02/Dec/20

Commented by Dwaipayan Shikari last updated on 02/Dec/20

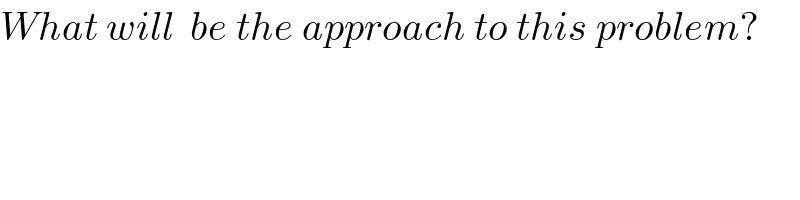
$${What}\:{will}\:\:{be}\:{the}\:{approach}\:{to}\:{this}\:{problem}? \\ $$

Answered by mindispower last updated on 03/Dec/20

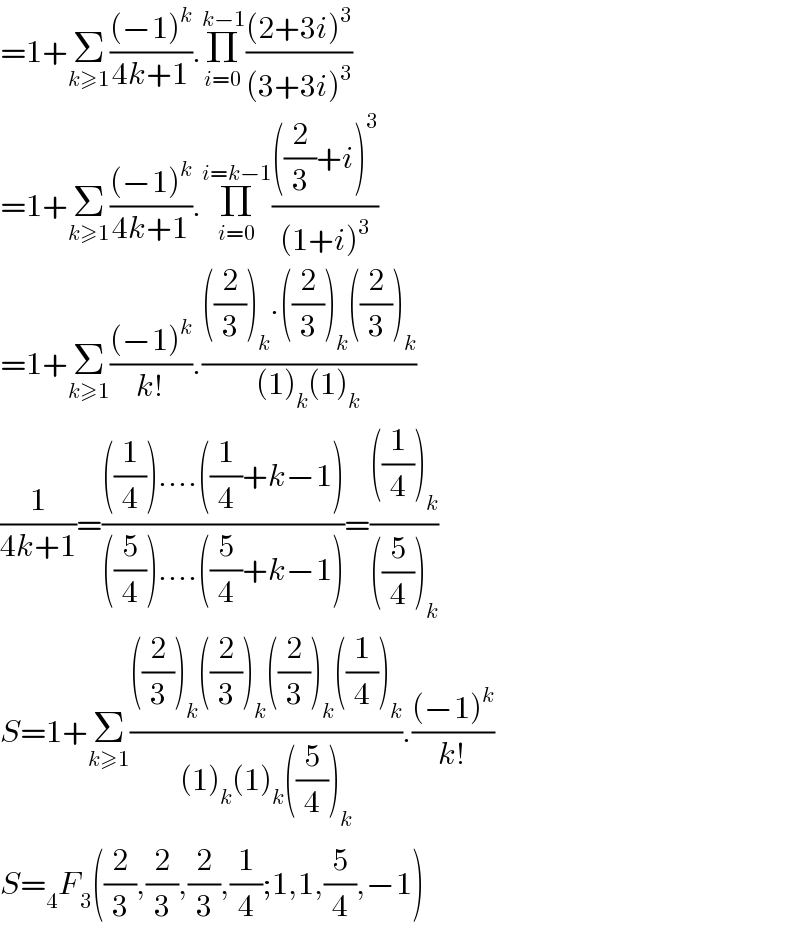
=1+Σ_(k≥1) (((−1)^k )/(4k+1)).Π_(i=0) ^(k−1) (((2+3i)^3 )/((3+3i)^3 )) =1+Σ_(k≥1) (((−1)^k )/(4k+1)).Π_(i=0) ^(i=k−1) ((((2/3)+i)^3 )/((1+i)^3 )) =1+Σ_(k≥1) (((−1)^k )/(k!)).((((2/3))_k .((2/3))_k ((2/3))_k )/((1)_k (1)_k )) (1/(4k+1))=((((1/4))....((1/4)+k−1))/(((5/4))....((5/4)+k−1)))=((((1/4))_k )/(((5/4))_k )) S=1+Σ_(k≥1) ((((2/3))_k ((2/3))_k ((2/3))_k ((1/4))_k )/((1)_k (1)_k ((5/4))_k )).(((−1)^k )/(k!)) S=_4 F_3 ((2/3),(2/3),(2/3),(1/4);1,1,(5/4),−1)

$$=\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{4}{k}+\mathrm{1}}.\underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\frac{\left(\mathrm{2}+\mathrm{3}{i}\right)^{\mathrm{3}} }{\left(\mathrm{3}+\mathrm{3}{i}\right)^{\mathrm{3}} } \\ $$$$=\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{4}{k}+\mathrm{1}}.\underset{{i}=\mathrm{0}} {\overset{{i}={k}−\mathrm{1}} {\prod}}\frac{\left(\frac{\mathrm{2}}{\mathrm{3}}+{i}\right)^{\mathrm{3}} }{\left(\mathrm{1}+{i}\right)^{\mathrm{3}} }\:\: \\ $$$$=\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!}.\frac{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)_{{k}} .\left(\frac{\mathrm{2}}{\mathrm{3}}\right)_{{k}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)_{{k}} }{\left(\mathrm{1}\right)_{{k}} \left(\mathrm{1}\right)_{{k}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{k}+\mathrm{1}}=\frac{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)….\left(\frac{\mathrm{1}}{\mathrm{4}}+{k}−\mathrm{1}\right)}{\left(\frac{\mathrm{5}}{\mathrm{4}}\right)….\left(\frac{\mathrm{5}}{\mathrm{4}}+{k}−\mathrm{1}\right)}=\frac{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{k}} }{\left(\frac{\mathrm{5}}{\mathrm{4}}\right)_{{k}} } \\ $$$${S}=\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)_{{k}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)_{{k}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)_{{k}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{k}} }{\left(\mathrm{1}\right)_{{k}} \left(\mathrm{1}\right)_{{k}} \left(\frac{\mathrm{5}}{\mathrm{4}}\right)_{{k}} }.\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!} \\ $$$${S}=_{\mathrm{4}} {F}_{\mathrm{3}} \left(\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{4}};\mathrm{1},\mathrm{1},\frac{\mathrm{5}}{\mathrm{4}},−\mathrm{1}\right) \\ $$

Commented by Dwaipayan Shikari last updated on 03/Dec/20

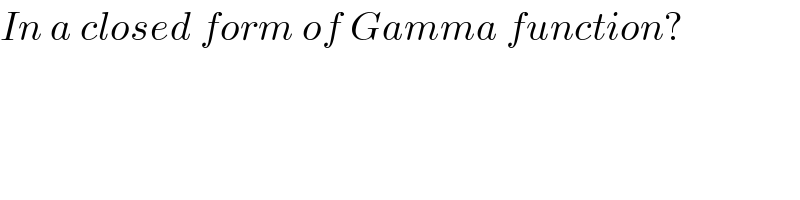
$${In}\:{a}\:{closed}\:{form}\:{of}\:{Gamma}\:{function}? \\ $$

Commented by mindispower last updated on 03/Dec/20

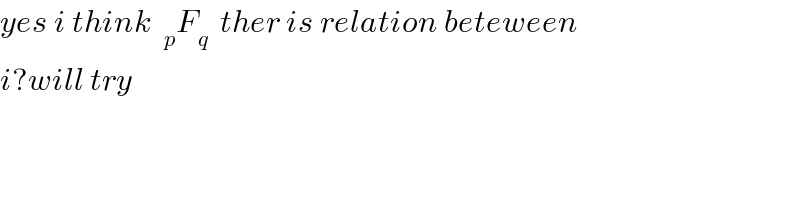
$${yes}\:{i}\:{think}\:\:_{{p}} {F}_{{q}} \:\:{ther}\:{is}\:{relation}\:{beteween} \\ $$$${i}?{will}\:{try} \\ $$$$ \\ $$

Commented by Dwaipayan Shikari last updated on 03/Dec/20

$${Thanking}\:{you} \\ $$

Commented by Dwaipayan Shikari last updated on 03/Dec/20

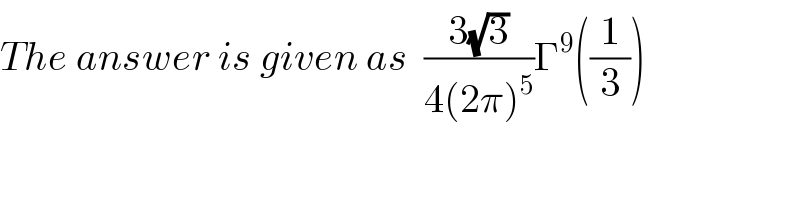
The answer is given as ((3(√3))/(4(2π)^5 ))Γ^9 ((1/3))

$${The}\:{answer}\:{is}\:{given}\:{as}\:\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}\left(\mathrm{2}\pi\right)^{\mathrm{5}} }\Gamma^{\mathrm{9}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply