Question Number 124389 by Engr_Jidda last updated on 03/Dec/20
Answered by Dwaipayan Shikari last updated on 03/Dec/20
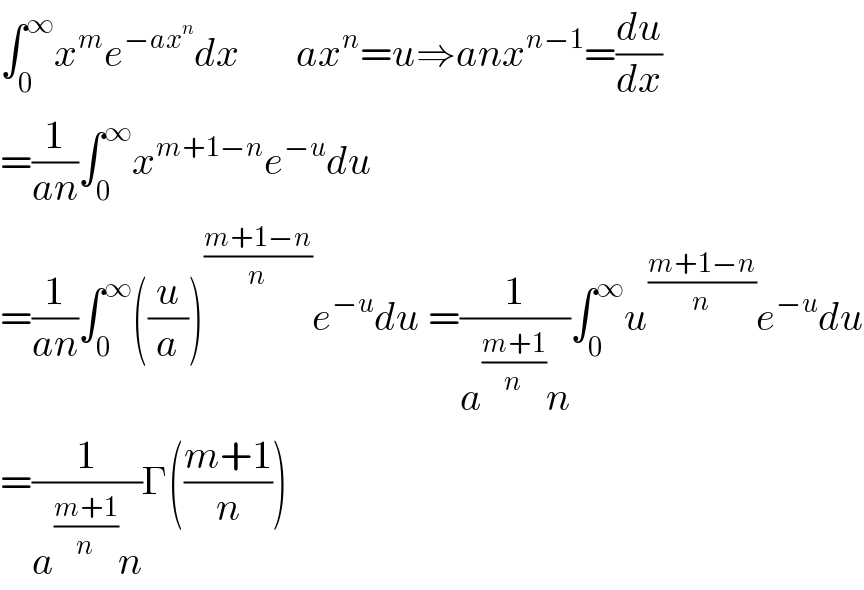
$$\int_{\mathrm{0}} ^{\infty} {x}^{{m}} {e}^{−{ax}^{{n}} } {dx}\:\:\:\:\:\:\:{ax}^{{n}} ={u}\Rightarrow{anx}^{{n}−\mathrm{1}} =\frac{{du}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{{an}}\int_{\mathrm{0}} ^{\infty} {x}^{{m}+\mathrm{1}−{n}} {e}^{−{u}} {du} \\ $$$$=\frac{\mathrm{1}}{{an}}\int_{\mathrm{0}} ^{\infty} \left(\frac{{u}}{{a}}\right)^{\frac{{m}+\mathrm{1}−{n}}{{n}}} {e}^{−{u}} {du}\:=\frac{\mathrm{1}}{{a}^{\frac{{m}+\mathrm{1}}{{n}}} {n}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{{m}+\mathrm{1}−{n}}{{n}}} {e}^{−{u}} {du} \\ $$$$=\frac{\mathrm{1}}{{a}^{\frac{{m}+\mathrm{1}}{{n}}} {n}}\Gamma\left(\frac{{m}+\mathrm{1}}{{n}}\right) \\ $$
Commented by Engr_Jidda last updated on 03/Dec/20

$$\mathrm{thank}\:\mathrm{you}?\mathrm{sir} \\ $$
