Question Number 131547 by liberty last updated on 06/Feb/21
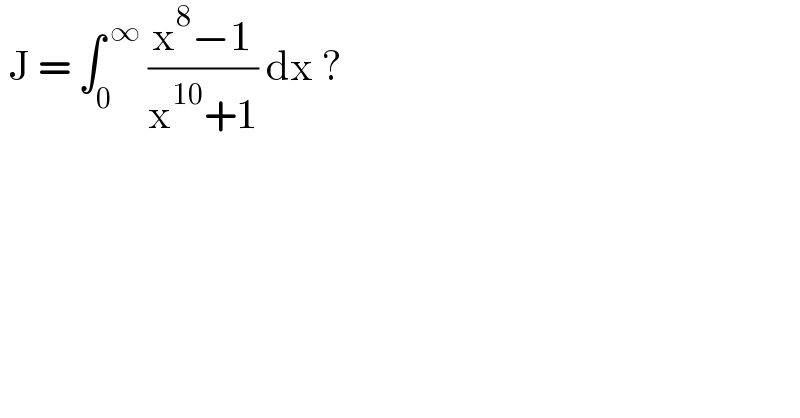
$$\:\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{x}^{\mathrm{8}} −\mathrm{1}}{\mathrm{x}^{\mathrm{10}} +\mathrm{1}}\:\mathrm{dx}\:? \\ $$
Answered by rs4089 last updated on 06/Feb/21

$$\mathrm{0} \\ $$
Answered by liberty last updated on 06/Feb/21
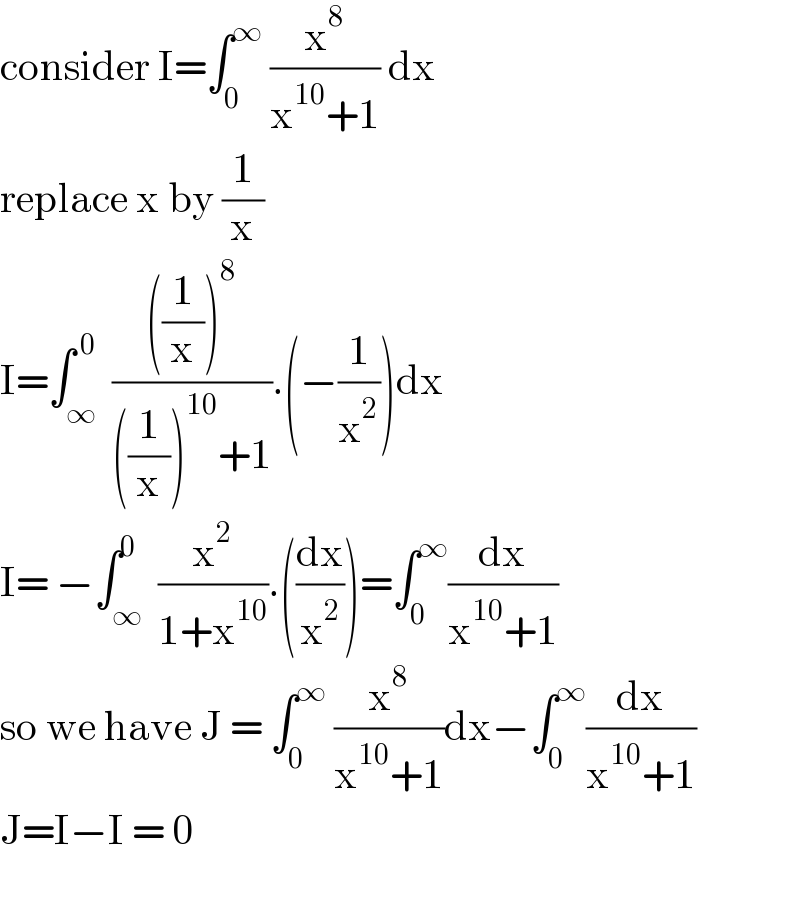
$$\mathrm{consider}\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{10}} +\mathrm{1}}\:\mathrm{dx}\: \\ $$$$\mathrm{replace}\:\mathrm{x}\:\mathrm{by}\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{I}=\int_{\infty} ^{\:\mathrm{0}} \:\frac{\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{8}} }{\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} +\mathrm{1}}.\left(−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$\mathrm{I}=\:−\int_{\infty} ^{\mathrm{0}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }.\left(\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{10}} +\mathrm{1}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{10}} +\mathrm{1}}\mathrm{dx}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{10}} +\mathrm{1}} \\ $$$$\mathrm{J}=\mathrm{I}−\mathrm{I}\:=\:\mathrm{0} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 06/Feb/21
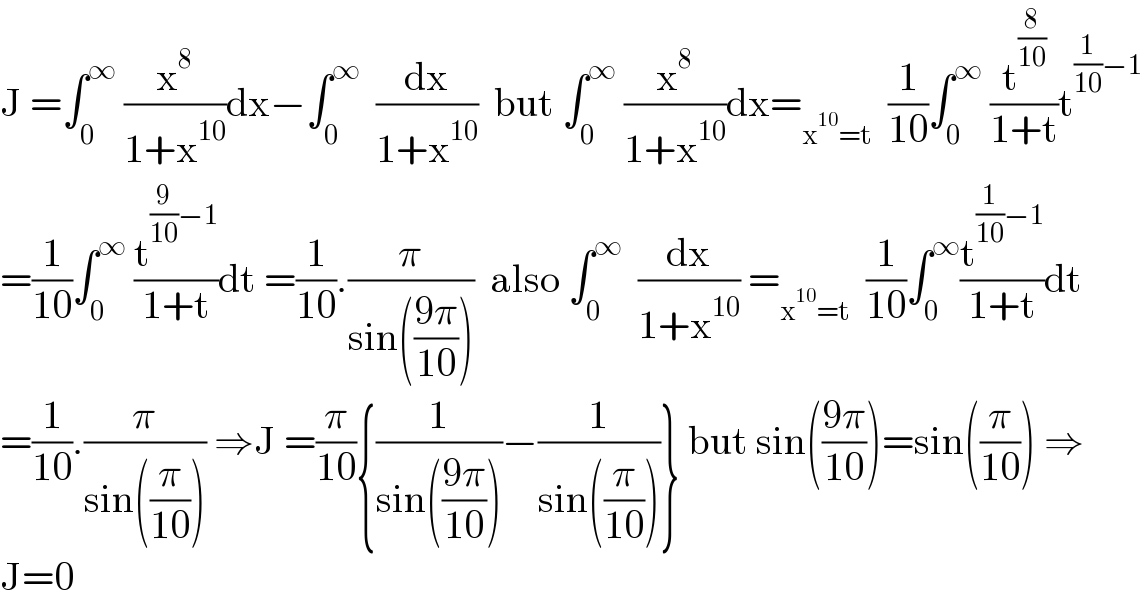
$$\mathrm{J}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }\:\:\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }\mathrm{dx}=_{\mathrm{x}^{\mathrm{10}} =\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{10}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{8}}{\mathrm{10}}} }{\mathrm{1}+\mathrm{t}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{10}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{9}}{\mathrm{10}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{10}}.\frac{\pi}{\mathrm{sin}\left(\frac{\mathrm{9}\pi}{\mathrm{10}}\right)}\:\:\mathrm{also}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }\:=_{\mathrm{x}^{\mathrm{10}} =\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{10}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{10}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}.\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)}\:\Rightarrow\mathrm{J}\:=\frac{\pi}{\mathrm{10}}\left\{\frac{\mathrm{1}}{\mathrm{sin}\left(\frac{\mathrm{9}\pi}{\mathrm{10}}\right)}−\frac{\mathrm{1}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)}\right\}\:\mathrm{but}\:\mathrm{sin}\left(\frac{\mathrm{9}\pi}{\mathrm{10}}\right)=\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)\:\Rightarrow \\ $$$$\mathrm{J}=\mathrm{0} \\ $$
