Question Number 124491 by Mammadli last updated on 03/Dec/20

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}^{{n}} }{{n}!}\:=\:\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 03/Dec/20
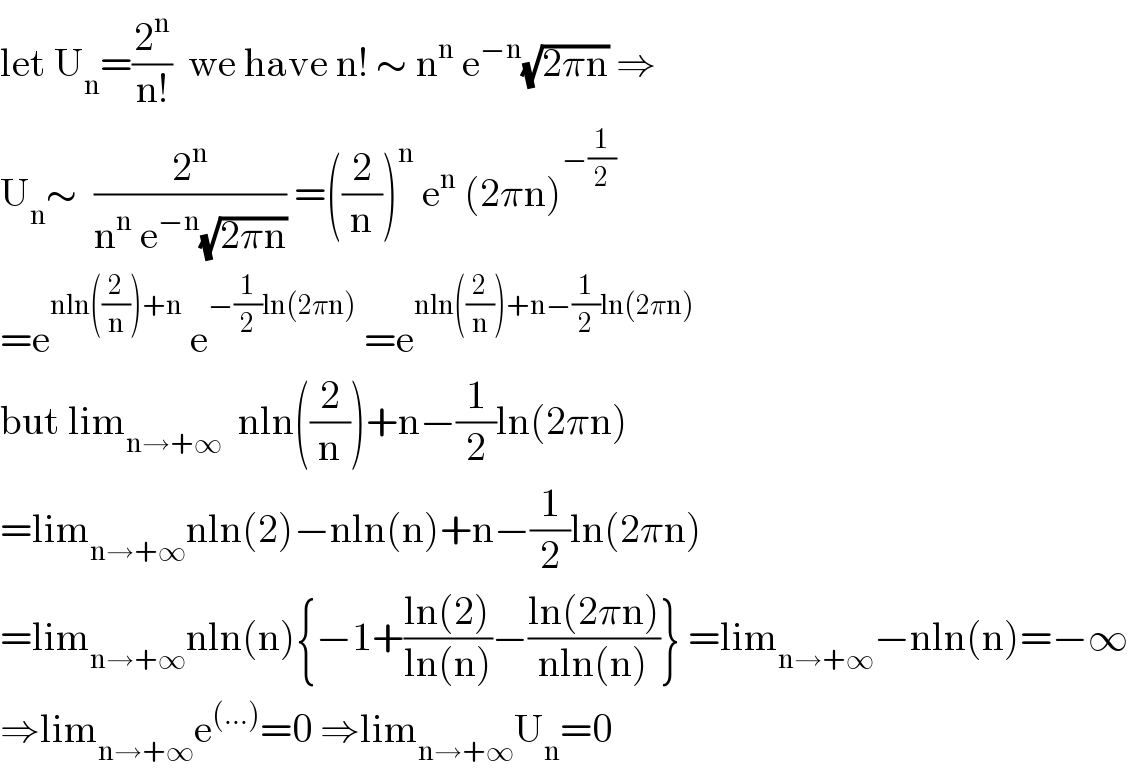
$$\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{n}!}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{n}!\:\sim\:\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\Rightarrow \\ $$$$\mathrm{U}_{\mathrm{n}} \sim\:\:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}}\:=\left(\frac{\mathrm{2}}{\mathrm{n}}\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{n}} \:\left(\mathrm{2}\pi\mathrm{n}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{e}^{\mathrm{nln}\left(\frac{\mathrm{2}}{\mathrm{n}}\right)+\mathrm{n}} \:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\pi\mathrm{n}\right)} \:=\mathrm{e}^{\mathrm{nln}\left(\frac{\mathrm{2}}{\mathrm{n}}\right)+\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\pi\mathrm{n}\right)} \\ $$$$\mathrm{but}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\mathrm{nln}\left(\frac{\mathrm{2}}{\mathrm{n}}\right)+\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\pi\mathrm{n}\right) \\ $$$$=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{nln}\left(\mathrm{2}\right)−\mathrm{nln}\left(\mathrm{n}\right)+\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\pi\mathrm{n}\right) \\ $$$$=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{nln}\left(\mathrm{n}\right)\left\{−\mathrm{1}+\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{ln}\left(\mathrm{n}\right)}−\frac{\mathrm{ln}\left(\mathrm{2}\pi\mathrm{n}\right)}{\mathrm{nln}\left(\mathrm{n}\right)}\right\}\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} −\mathrm{nln}\left(\mathrm{n}\right)=−\infty\: \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{e}^{\left(…\right)} =\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{U}_{\mathrm{n}} =\mathrm{0} \\ $$
Answered by mr W last updated on 04/Dec/20
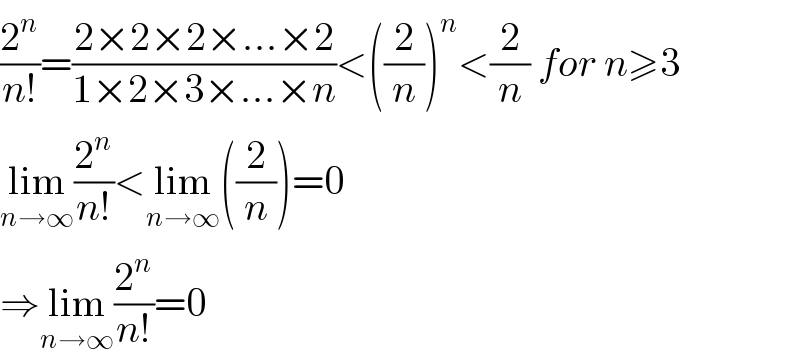
$$\frac{\mathrm{2}^{{n}} }{{n}!}=\frac{\mathrm{2}×\mathrm{2}×\mathrm{2}×…×\mathrm{2}}{\mathrm{1}×\mathrm{2}×\mathrm{3}×…×{n}}<\left(\frac{\mathrm{2}}{{n}}\right)^{{n}} <\frac{\mathrm{2}}{{n}}\:{for}\:{n}\geqslant\mathrm{3} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}^{{n}} }{{n}!}<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}}{{n}}\right)=\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}^{{n}} }{{n}!}=\mathrm{0} \\ $$
