Question Number 124718 by Dwaipayan Shikari last updated on 05/Dec/20
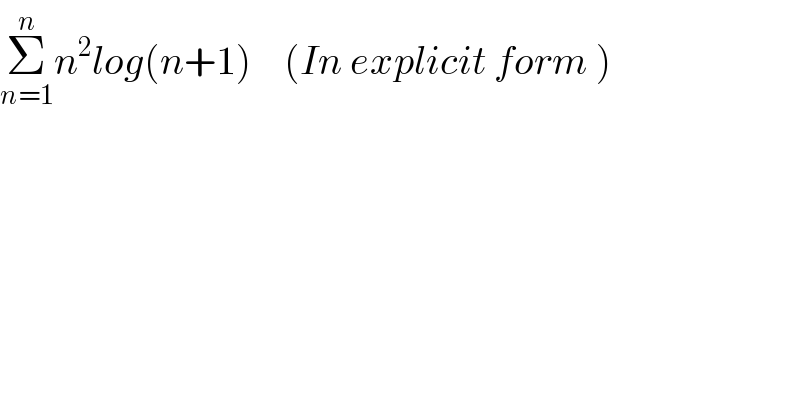
$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n}^{\mathrm{2}} {log}\left({n}+\mathrm{1}\right)\:\:\:\:\left({In}\:{explicit}\:{form}\:\right) \\ $$
Commented by Dwaipayan Shikari last updated on 05/Dec/20
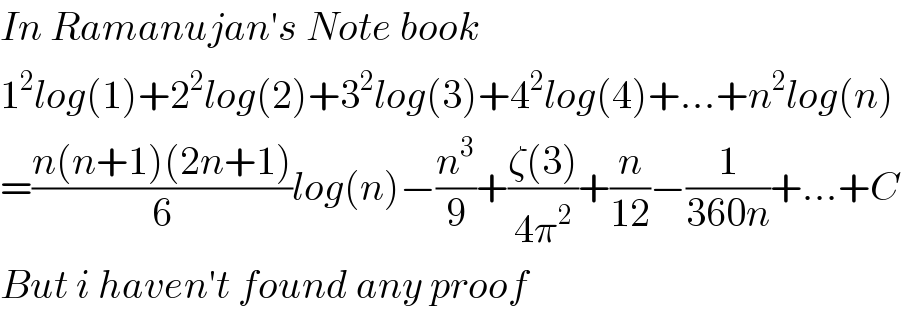
$${In}\:{Ramanujan}'{s}\:{Note}\:{book} \\ $$$$\mathrm{1}^{\mathrm{2}} {log}\left(\mathrm{1}\right)+\mathrm{2}^{\mathrm{2}} {log}\left(\mathrm{2}\right)+\mathrm{3}^{\mathrm{2}} {log}\left(\mathrm{3}\right)+\mathrm{4}^{\mathrm{2}} {log}\left(\mathrm{4}\right)+…+{n}^{\mathrm{2}} {log}\left({n}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}{log}\left({n}\right)−\frac{{n}^{\mathrm{3}} }{\mathrm{9}}+\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{4}\pi^{\mathrm{2}} }+\frac{{n}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{360}{n}}+…+{C}\:\: \\ $$$${But}\:{i}\:{haven}'{t}\:{found}\:{any}\:{proof}\: \\ $$
