Question Number 124723 by mnjuly1970 last updated on 05/Dec/20
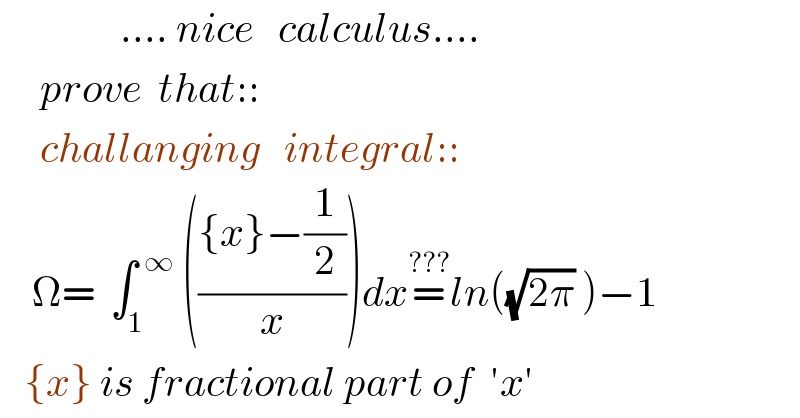
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:{nice}\:\:\:{calculus}…. \\ $$$$\:\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\:\:{challanging}\:\:\:{integral}:: \\ $$$$\:\:\:\:\Omega=\:\:\int_{\mathrm{1}} ^{\:\:\infty} \:\left(\frac{\left\{{x}\right\}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}}\right){dx}\overset{???} {=}{ln}\left(\sqrt{\mathrm{2}\pi}\:\right)−\mathrm{1} \\ $$$$\:\:\:\left\{{x}\right\}\:{is}\:{fractional}\:{part}\:{of}\:\:'{x}' \\ $$
Answered by Bird last updated on 05/Dec/20
![Ω=∫_1 ^∞ ((x−[x]−(1/2))/x)dx =∫_1 ^∞ (1−(([x]+(1/2))/x))dx =Σ_(n=1) ^∞ ∫_n ^(n+1) (1−((n+(1/2))/x))dx =Σ_(n=1) ^∞ ∫_n ^(n+1) dx−(n+(1/2))(dx/x) =Σ_(n=1) ^∞ (1−(n+(1/2)){ln(n+1)−ln(n)} =Σ_(n=1) ^∞ (1−(n+(1/2))ln(1+(1/n))) ln^′ (1+u)=1−u+o(u^2 ) ⇒ ln(1+u)=u−(u^2 /2) +o(u^2 ) ⇒ ln(1+(1/n))=(1/n)−(1/(2n^2 ))+o((1/n^2 ))⇒ 1−(n+(1/2))ln(1+(1/n)) ∼1−(n+(1/2))((1/n)−(1/(2n^2 ))) 1−(1−(1/(2n))+(1/(2n))−(1/(4n^2 )))=(1/(4n^2 )) ⇒ Σ_(n=1) ^∞ {1−(n+(1/2))ln(1+(1/n))} is convergent...be continued](https://www.tinkutara.com/question/Q124765.png)
$$\Omega=\int_{\mathrm{1}} ^{\infty} \frac{{x}−\left[{x}\right]−\frac{\mathrm{1}}{\mathrm{2}}}{{x}}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{\left[{x}\right]+\frac{\mathrm{1}}{\mathrm{2}}}{{x}}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \left(\mathrm{1}−\frac{{n}+\frac{\mathrm{1}}{\mathrm{2}}}{{x}}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} {dx}−\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{{dx}}{{x}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left\{{ln}\left({n}+\mathrm{1}\right)−{ln}\left({n}\right)\right\}\right. \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\right) \\ $$$${ln}^{'} \left(\mathrm{1}+{u}\right)=\mathrm{1}−{u}+{o}\left({u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\Rightarrow \\ $$$$\mathrm{1}−\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right) \\ $$$$\sim\mathrm{1}−\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \left\{\mathrm{1}−\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\right\} \\ $$$${is}\:{convergent}…{be}\:{continued} \\ $$
