Question Number 124794 by benjo_mathlover last updated on 06/Dec/20
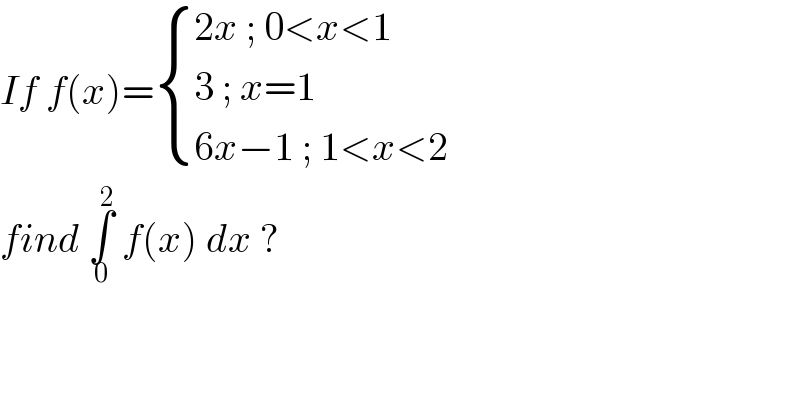
$${If}\:{f}\left({x}\right)=\begin{cases}{\mathrm{2}{x}\:;\:\mathrm{0}<{x}<\mathrm{1}}\\{\mathrm{3}\:;\:{x}=\mathrm{1}\:}\\{\mathrm{6}{x}−\mathrm{1}\:;\:\mathrm{1}<{x}<\mathrm{2}}\end{cases} \\ $$$${find}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right)\:{dx}\:? \\ $$
Answered by TITA last updated on 06/Dec/20
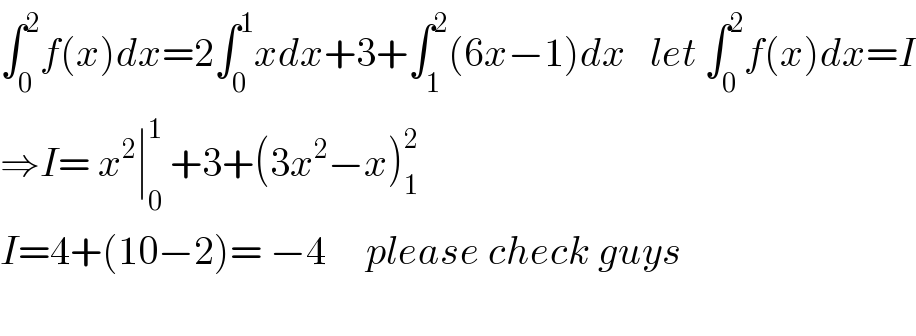
$$\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {xdx}+\mathrm{3}+\int_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{6}{x}−\mathrm{1}\right){dx}\:\:\:{let}\:\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({x}\right){dx}={I} \\ $$$$\Rightarrow{I}=\:{x}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{1}} \:+\mathrm{3}+\left(\mathrm{3}{x}^{\mathrm{2}} −{x}\right)_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${I}=\mathrm{4}+\left(\mathrm{10}−\mathrm{2}\right)=\:−\mathrm{4}\:\:\:\:\:{please}\:{check}\:{guys} \\ $$$$ \\ $$
