Question Number 124916 by liberty last updated on 07/Dec/20
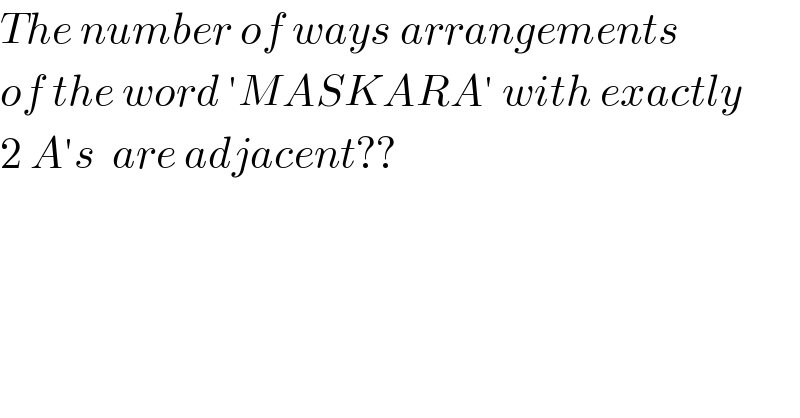
$${The}\:{number}\:{of}\:{ways}\:{arrangements}\: \\ $$$${of}\:{the}\:{word}\:'{MASKARA}'\:{with}\:{exactly} \\ $$$$\mathrm{2}\:{A}'{s}\:\:{are}\:{adjacent}??\: \\ $$
Answered by mr W last updated on 07/Dec/20

$$\_\mathrm{M\_S\_K\_R\_} \\ $$$$\mathrm{4}!×{P}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{480} \\ $$
Commented by mr W last updated on 07/Dec/20
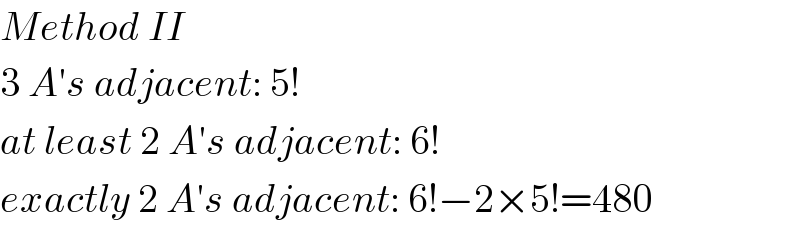
$${Method}\:{II} \\ $$$$\mathrm{3}\:{A}'{s}\:{adjacent}:\:\mathrm{5}! \\ $$$${at}\:{least}\:\mathrm{2}\:{A}'{s}\:{adjacent}:\:\mathrm{6}! \\ $$$${exactly}\:\mathrm{2}\:{A}'{s}\:{adjacent}:\:\mathrm{6}!−\mathrm{2}×\mathrm{5}!=\mathrm{480} \\ $$
Commented by bemath last updated on 07/Dec/20
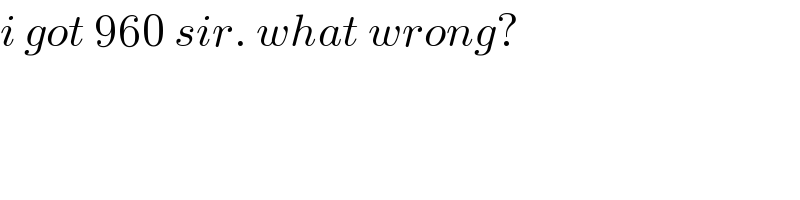
$${i}\:{got}\:\mathrm{960}\:{sir}.\:{what}\:{wrong}? \\ $$
Commented by mr W last updated on 07/Dec/20

$${how}\:{did}\:{you}\:{get}? \\ $$
Answered by liberty last updated on 07/Dec/20

$$\left(\bullet\right)\:\underset{\mathrm{1}^{{st}} } {−}\:\overset{{AA}} {−}\:\underset{\mathrm{2}^{{nd}} } {−}\:\overset{{A}} {−}\:\underset{\mathrm{3}^{{rd}} } {−} \\ $$$$\:{Treat}\:\mathrm{4}\:{letters}\:{M}\:,{S},\:{K},\:{R}\:{as}\:{identical}\:'{x}' \\ $$$${since}\:{exactly}\:\mathrm{2}\:{A}'{s}\:{are}\:{adjacent},\:{one}\:{x}\:{must}\:{be} \\ $$$${put}\:{in}\:\mathrm{2}^{{nd}} \:{places}\:\Rightarrow\:\underset{\mathrm{1}^{{st}} } {−}\:{AA}\:\underset{\mathrm{2}^{{nd}} } {\overset{{x}} {−}}\:{A}\:\underset{\mathrm{3}^{{rx}} } {−} \\ $$$${the}\:{remaining}\:\mathrm{3}\:{x}'{s}\:{can}\:{be}\:{put}\:{in}\:\begin{pmatrix}{\mathrm{3}+\mathrm{3}−\mathrm{1}}\\{\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}\:=\:\mathrm{10} \\ $$$$\left(\bullet\bullet\right)\:\underset{\mathrm{1}^{{st}} } {−}\:{A}\:\underset{\mathrm{2}^{{nd}} } {−}\:{AA}\:\underset{\mathrm{3}^{{rd}} } {−}\:{similar}\:{to}\:{cases}\:\left(\bullet\right) \\ $$$${therefore}\:{the}\:{desired}\:{number}\:{of}\:{ways} \\ $$$${is}\:{given}\:{by}\:\mathrm{2}×\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}×\mathrm{4}!\:=\:\mathrm{20}×\mathrm{24}\:=\:\mathrm{480} \\ $$
