Question Number 5876 by sanusihammed last updated on 03/Jun/16

Commented by Yozzii last updated on 04/Jun/16
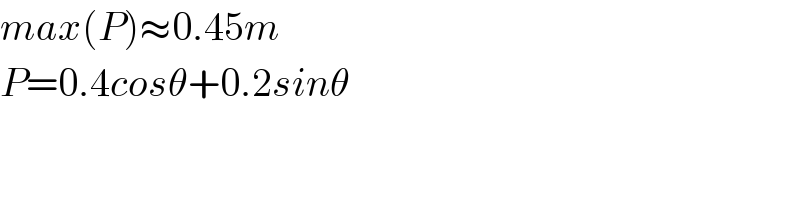
$${max}\left({P}\right)\approx\mathrm{0}.\mathrm{45}{m} \\ $$$${P}=\mathrm{0}.\mathrm{4}{cos}\theta+\mathrm{0}.\mathrm{2}{sin}\theta \\ $$
Commented by sanusihammed last updated on 04/Jun/16
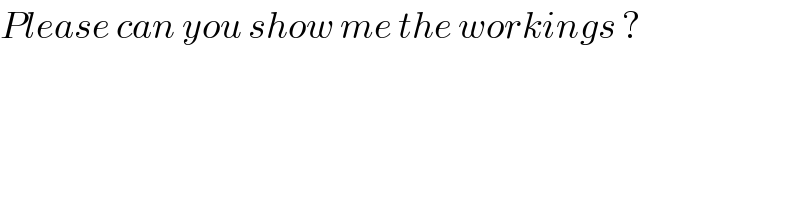
$${Please}\:{can}\:{you}\:{show}\:{me}\:{the}\:{workings}\:? \\ $$
Answered by Rasheed Soomro last updated on 09/Jun/16
Commented by Rasheed Soomro last updated on 09/Jun/16
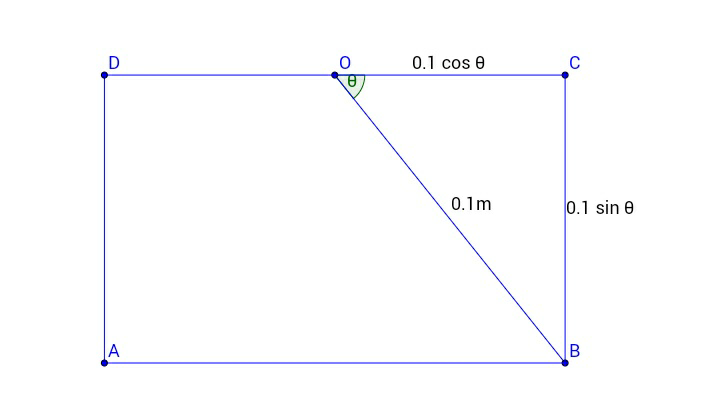
![Perimeter=2(∣BC∣+∣CD∣) =2(2∣OC∣+∣CD∣) =2[2(0.1cosθ)+0.1sinθ] =2[0.2cosθ+0.1sinθ] Now, (√(0.2^2 +0.1^2 ))=((√5)/(10)) =2×((√5)/(10))[(2/( (√5)))cosθ+(1/( (√5)))sinθ] =((√5)/5)[(2/( (√5)))cosθ+(1/( (√5)))sinθ] =((√5)/5)[sin(θ+∅)] Where sin ∅=(2/( (√5))) and cos ∅=(1/( (√5))) I can′t continue.](https://www.tinkutara.com/question/Q6003.png)
$${Perimeter}=\mathrm{2}\left(\mid{BC}\mid+\mid{CD}\mid\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{2}\mid{OC}\mid+\mid{CD}\mid\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left[\mathrm{2}\left(\mathrm{0}.\mathrm{1}{cos}\theta\right)+\mathrm{0}.\mathrm{1}{sin}\theta\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left[\mathrm{0}.\mathrm{2}{cos}\theta+\mathrm{0}.\mathrm{1}{sin}\theta\right] \\ $$$$\:\:\:\:\:{Now},\:\:\:\:\:\sqrt{\mathrm{0}.\mathrm{2}^{\mathrm{2}} +\mathrm{0}.\mathrm{1}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}×\frac{\sqrt{\mathrm{5}}}{\mathrm{10}}\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}{cos}\theta+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}{sin}\theta\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}{cos}\theta+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}{sin}\theta\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\left[{sin}\left(\theta+\emptyset\right)\right] \\ $$$$\:\:\:\:\:\:{Where}\:{sin}\:\emptyset=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:{and}\:{cos}\:\emptyset=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${I}\:{can}'{t}\:{continue}. \\ $$$$ \\ $$
