Menu Close

lim-n-n-0-pi-2-cos-2n-1-d-

Tinku Tara 0 Comments
Pin




Question Number 131548 by liberty last updated on 06/Feb/21
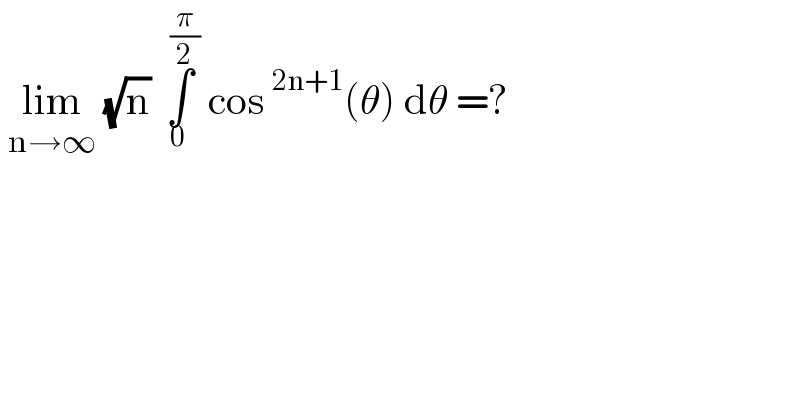
lim_(n→∞) (√n) ∫_0 ^( (π/2)) cos^(2n+1) (θ) dθ =?
$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{n}}\:\underset{\mathrm{0}} {\overset{\:\:\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{cos}\:^{\mathrm{2n}+\mathrm{1}} \left(\theta\right)\:\mathrm{d}\theta\:=? \\ $$
Answered by rs4089 last updated on 06/Feb/21
((π(√π))/2)
$$\frac{\pi\sqrt{\pi}}{\mathrm{2}} \\ $$
Commented by liberty last updated on 06/Feb/21
False
$$\mathrm{False} \\ $$
Answered by liberty last updated on 06/Feb/21
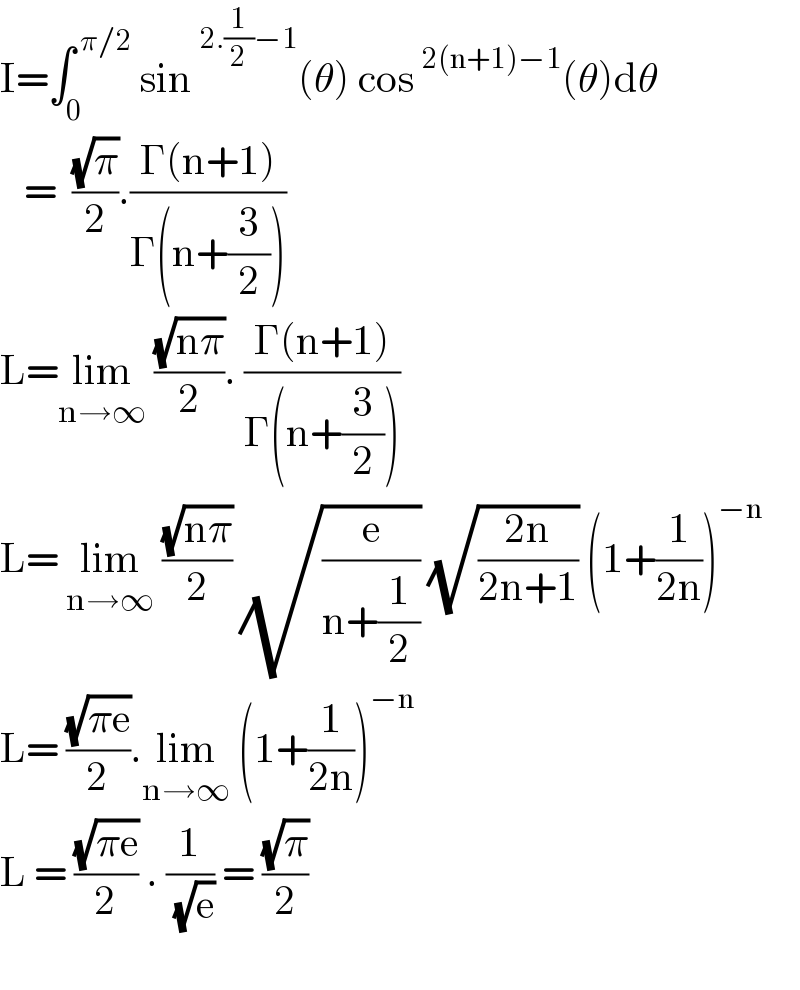
I=∫_0 ^( π/2) sin^(2.(1/2)−1) (θ) cos^(2(n+1)−1) (θ)dθ = ((√π)/2).((Γ(n+1))/(Γ(n+(3/2)))) L=lim_(n→∞) ((√(nπ))/2). ((Γ(n+1))/(Γ(n+(3/2)))) L= lim_(n→∞) ((√(nπ))/2) (√(e/(n+(1/2)))) (√((2n)/(2n+1))) (1+(1/(2n)))^(−n) L= ((√(πe))/2).lim_(n→∞) (1+(1/(2n)))^(−n) L = ((√(πe))/2) . (1/( (√e))) = ((√π)/2)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\mathrm{sin}\:^{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\theta\right)\:\mathrm{cos}\:^{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{1}} \left(\theta\right)\mathrm{d}\theta \\ $$$$\:\:\:=\:\:\frac{\sqrt{\pi}}{\mathrm{2}}.\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\mathrm{L}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{n}\pi}}{\mathrm{2}}.\:\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\mathrm{L}=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{n}\pi}}{\mathrm{2}}\:\sqrt{\frac{\mathrm{e}}{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}}}\:\sqrt{\frac{\mathrm{2n}}{\mathrm{2n}+\mathrm{1}}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}\right)^{−\mathrm{n}} \\ $$$$\mathrm{L}=\:\frac{\sqrt{\pi\mathrm{e}}}{\mathrm{2}}.\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}\right)^{−\mathrm{n}} \\ $$$$\mathrm{L}\:=\:\frac{\sqrt{\pi\mathrm{e}}}{\mathrm{2}}\:.\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}}\:=\:\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by rs4089 last updated on 06/Feb/21
thank you very much sir i got my mistake:)
$${thank}\:{you}\:{very}\:{much}\:{sir}\: \\ $$$$\left.{i}\:{got}\:{my}\:{mistake}:\right) \\ $$
Answered by rs4089 last updated on 06/Feb/21
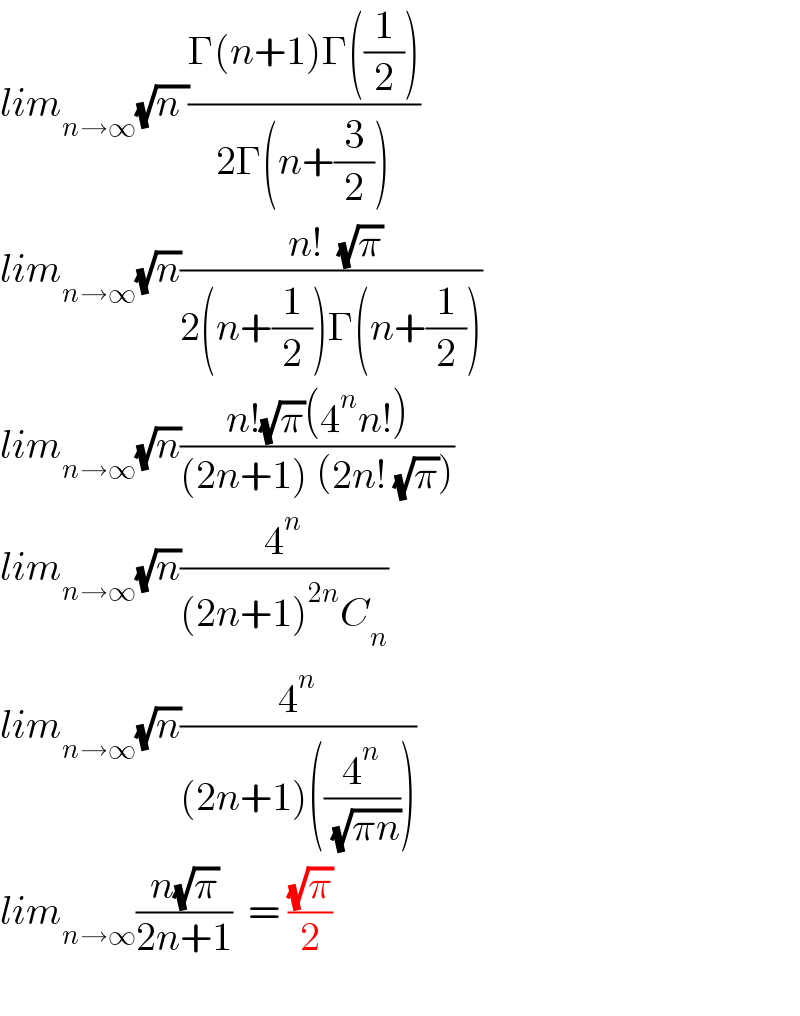
lim_(n→∞) (√(n ))((Γ(n+1)Γ((1/2)))/(2Γ(n+(3/2)))) lim_(n→∞) (√n)(( n! (√π))/(2(n+(1/2))Γ(n+(1/2)))) lim_(n→∞) (√n)((n!(√π)(4^n n!))/((2n+1) (2n! (√π)))) lim_(n→∞) (√n)(4^n /((2n+1)^(2n) C_n )) lim_(n→∞) (√n)(4^n /((2n+1)((4^n /( (√(πn))))))) lim_(n→∞) ((n(√π))/(2n+1)) = ((√π)/2)
$${lim}_{{n}\rightarrow\infty} \sqrt{{n}\:}\frac{\Gamma\left({n}+\mathrm{1}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$${lim}_{{n}\rightarrow\infty} \sqrt{{n}}\frac{\:{n}!\:\:\sqrt{\pi}}{\mathrm{2}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${lim}_{{n}\rightarrow\infty} \sqrt{{n}}\frac{{n}!\sqrt{\pi}\left(\mathrm{4}^{{n}} {n}!\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)\:\left(\mathrm{2}{n}!\:\sqrt{\pi}\right)} \\ $$$${lim}_{{n}\rightarrow\infty} \sqrt{{n}}\frac{\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}{n}} {C}_{{n}} } \\ $$$${lim}_{{n}\rightarrow\infty} \sqrt{{n}}\frac{\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\frac{\mathrm{4}^{{n}} }{\:\sqrt{\pi{n}}}\right)} \\ $$$${lim}_{{n}\rightarrow\infty} \frac{{n}\sqrt{\pi}}{\mathrm{2}{n}+\mathrm{1}}\:\:=\:\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 06/Feb/21
let W_n =∫_0 ^(π/2) cos^(2n+1) θ dθ ⇒W_n =∫_0 ^(π/2) cos^(2n+1) θ .sin^(2.(1/2)−1) θdθ =∫_0 ^(π/2) cos^(2(n+1)−1) θ sin^(2.(1/2)−1) θdθ =(1/2)B(n+1,(1/2)) =(1/2).((Γ(n+1).Γ((1/2)))/(Γ(n+(3/2)))) =((√π)/2).((n!)/(Γ(n+(3/2)))) we have n! ∼n^n .e^(−n) (√(2πn)) and Γ(n+(1/2)+1) =(n+(1/2))!∼(n+(1/2))^(n+(1/2)) e^(−(n+(1/2))) (√(2π(n+(1/2)))) ⇒((n!)/(Γ(n+(3/2))))∼((n^n .e^(−n) (√(2πn)))/((n+(1/2))^(n+(1/2)) e^(−n) .e^(−(1/2)) (√(2π)).(√(n+(1/2))))) =(√e).(n^(n+(1/2)) /((n+(1/2))^(n+1) )) ⇒(√n)W_n ∼ (√e).(n^(n+1) /((n+(1/2))^(n+1) )) =(√e).((n/(n+1)))^(n+1) =(√e)e^((n+1)log(((n+1−1)/(n+1)))) =(√e)e^((n+1)log(1−(1/(n+1)))) =(√e).e^(−1) =(1/( (√e))) ⇒lim_(n→+∞) nW_n =(1/( (√e)))
$$\mathrm{let}\:\:\mathrm{W}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \theta\:\mathrm{d}\theta\:\Rightarrow\mathrm{W}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \theta\:.\mathrm{sin}^{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \theta\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{1}} \theta\:\mathrm{sin}^{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \theta\mathrm{d}\theta\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\mathrm{n}+\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\:=\frac{\sqrt{\pi}}{\mathrm{2}}.\frac{\mathrm{n}!}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{n}!\:\sim\mathrm{n}^{\mathrm{n}} .\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\:\mathrm{and}\:\Gamma\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\:=\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)!\sim\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \sqrt{\mathrm{2}\pi\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\: \\ $$$$\Rightarrow\frac{\mathrm{n}!}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\sim\frac{\mathrm{n}^{\mathrm{n}} .\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}}{\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{n}} .\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{2}\pi}.\sqrt{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}}} \\ $$$$=\sqrt{\mathrm{e}}.\frac{\mathrm{n}^{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} }\:\Rightarrow\sqrt{\mathrm{n}}\mathrm{W}_{\mathrm{n}} \sim\:\sqrt{\mathrm{e}}.\frac{\mathrm{n}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} } \\ $$$$=\sqrt{\mathrm{e}}.\left(\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{n}+\mathrm{1}} \:=\sqrt{\mathrm{e}}\mathrm{e}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{log}\left(\frac{\mathrm{n}+\mathrm{1}−\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)} \:=\sqrt{\mathrm{e}}\mathrm{e}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)} \\ $$$$=\sqrt{\mathrm{e}}.\mathrm{e}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{nW}_{\mathrm{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}} \\ $$
Commented by mathmax by abdo last updated on 06/Feb/21
sorry lim_(n→+∞) nW_n =((√π)/2).(1/( (√e))) =((√π)/(2(√e)))
$$\mathrm{sorry}\:\:\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{nW}_{\mathrm{n}} =\frac{\sqrt{\pi}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{e}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *