Question Number 125462 by mnjuly1970 last updated on 11/Dec/20
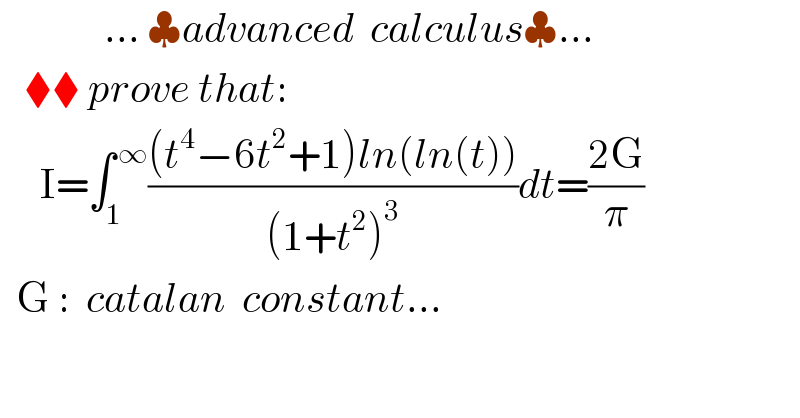
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…\:\clubsuit{advanced}\:\:{calculus}\clubsuit… \\ $$$$\:\:\:\blacklozenge\blacklozenge\:{prove}\:{that}: \\ $$$$\:\:\:\:\:\mathrm{I}=\int_{\mathrm{1}} ^{\:\infty} \frac{\left({t}^{\mathrm{4}} −\mathrm{6}{t}^{\mathrm{2}} +\mathrm{1}\right){ln}\left({ln}\left({t}\right)\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }{dt}=\frac{\mathrm{2G}}{\pi} \\ $$$$\:\:\mathrm{G}\::\:\:{catalan}\:\:{constant}… \\ $$
Answered by mindispower last updated on 13/Dec/20
$${helllo}\:{sir}\:{sur}\:{for}\:{this}\:{result}? \\ $$
Commented by mnjuly1970 last updated on 16/Dec/20

$$\:\:\:\:{source}\:\::{wikipedia}…{catalan}\: \\ $$$${constant}\:..{integral}\:\:{representation}… \\ $$
Commented by mindispower last updated on 16/Dec/20
$${hello}\:{sir}\:{ok}\:{i}\:{wiil}?{try}\:{it} \\ $$
Commented by mnjuly1970 last updated on 16/Dec/20

$$\:\:{sincerly}\:{yours}… \\ $$
