Question Number 191076 by Mingma last updated on 17/Apr/23
Answered by mr W last updated on 18/Apr/23

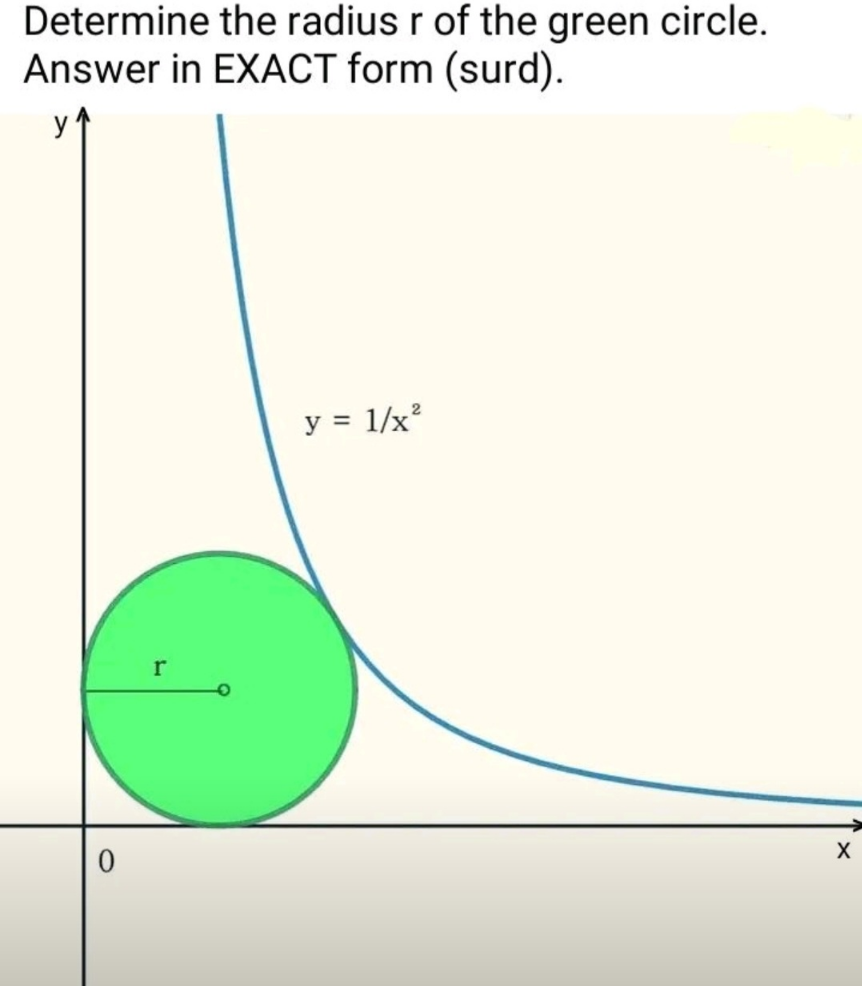
$${touching}\:{point}\:{P}\left({p},\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\right) \\ $$$$\mathrm{tan}\:\theta=−\frac{{dy}}{{dx}}=\frac{\mathrm{2}}{{p}^{\mathrm{3}} } \\ $$$${r}={p}−{r}\:\mathrm{sin}\:\theta={p}−\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{4}+{p}^{\mathrm{6}} }} \\ $$$$\Rightarrow{r}=\frac{{p}}{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{p}^{\mathrm{6}} }}} \\ $$$${r}=\frac{\mathrm{1}}{{p}^{\mathrm{2}} }−{r}\:\mathrm{cos}\:\theta=\frac{\mathrm{1}}{{p}^{\mathrm{2}} }−\frac{{rp}^{\mathrm{3}} }{\:\sqrt{\mathrm{4}+{p}^{\mathrm{6}} }} \\ $$$$\Rightarrow{r}=\frac{\mathrm{1}}{{p}^{\mathrm{2}} \left(\mathrm{1}+\frac{{p}^{\mathrm{3}} }{\:\sqrt{\mathrm{4}+{p}^{\mathrm{6}} }}\right)} \\ $$$$\frac{{p}}{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{p}^{\mathrm{6}} }}}=\frac{\mathrm{1}}{{p}^{\mathrm{2}} \left(\mathrm{1}+\frac{{p}^{\mathrm{3}} }{\:\sqrt{\mathrm{4}+{p}^{\mathrm{6}} }}\right)} \\ $$$${let}\:{t}={p}^{\mathrm{3}} \\ $$$$\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{t}^{\mathrm{2}} }}={t}\left(\mathrm{1}+\frac{{t}}{\:\sqrt{\mathrm{4}+{t}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{2}−{t}^{\mathrm{2}} =\left({t}−\mathrm{1}\right)\sqrt{\mathrm{4}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}{t}^{\mathrm{2}} −\mathrm{9}{t}+\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{9}−\sqrt{\mathrm{17}}}{\mathrm{4}}={p}^{\mathrm{3}} \\ $$$$\Rightarrow{p}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{9}−\sqrt{\mathrm{17}}}{\mathrm{4}}} \\ $$$$\Rightarrow{r}=\frac{\sqrt[{\mathrm{3}}]{\frac{\mathrm{9}−\sqrt{\mathrm{17}}}{\mathrm{4}}}}{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+\left(\frac{\mathrm{9}−\sqrt{\mathrm{17}}}{\mathrm{4}}\right)^{\mathrm{2}} }}}\approx\mathrm{0}.\mathrm{57626} \\ $$
Commented by mehdee42 last updated on 18/Apr/23

$${very}\:{nice} \\ $$
Commented by mr W last updated on 18/Apr/23

Commented by Mingma last updated on 18/Apr/23
Excellent, sir!
