Menu Close

Question-125577

Tinku Tara 0 Comments
Pin




Question Number 125577 by ajfour last updated on 12/Dec/20
Commented by ajfour last updated on 12/Dec/20
If the cubic curve′s eq. is y=x^3 −x−c and parabola′s eq. is y=(x−h)^2 +((2/(3(√3)))−c) , then with the help of a suitable values of h and s, find the positive root, x=p of the cubic.
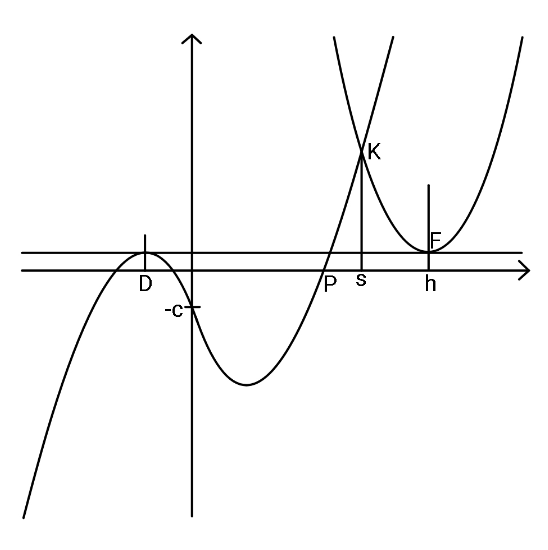
$${If}\:{the}\:{cubic}\:{curve}'{s}\:{eq}.\:\:{is} \\ $$$${y}={x}^{\mathrm{3}} −{x}−{c} \\ $$$${and}\:{parabola}'{s}\:{eq}.\:{is}\: \\ $$$${y}=\left({x}−{h}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}−{c}\right)\:,\:{then} \\ $$$${with}\:{the}\:{help}\:{of}\:{a}\:{suitable}\:{values} \\ $$$${of}\:{h}\:{and}\:{s}, \\ $$$${find}\:{the}\:{positive}\:{root},\:\:{x}={p} \\ $$$${of}\:{the}\:{cubic}. \\ $$
Answered by ajfour last updated on 12/Dec/20
y=x^3 −x−c y=(x−h)^2 +k p^3 =p+c ..(i) (s−h)^2 +k=s^3 −s−c let s=p+m ⇒ p^3 +3mp^2 +3m^2 p+m^3 −p−m−c−k −p^2 −2mp−m^2 +2hp+2mh−h^2 =0 let 3m=1_(−) ⇒ p(2h−(1/3))−(8/(27))−k−(h−(1/3))^2 =0 ⇒ p=(((h−(1/3))^2 +k+(8/(27)))/(2h−(1/3))) but p^3 =p+c ⇒ {(h−(1/3))^2 +k+(8/(27))}^3 ={(h−(1/3))^2 +k+(8/(27))}(2h−(1/3))^2 +c(2h−(1/3))^3 let k=((2h)/3) (h^2 +((11)/(27)))^3 =(h^2 +((11)/(27)))(2h−(1/3))^2 +c(2h−(1/3))^3 (h^2 +((11)/(27)))(h^4 +((22h^2 )/(27))+((121)/(729))−4h^2 +((4h)/3)−(1/9)) =c(2h−(1/3))^3 .....
$${y}={x}^{\mathrm{3}} −{x}−{c} \\ $$$${y}=\left({x}−{h}\right)^{\mathrm{2}} +{k}\:\: \\ $$$${p}^{\mathrm{3}} ={p}+{c}\:\:..\left({i}\right) \\ $$$$\left({s}−{h}\right)^{\mathrm{2}} +{k}={s}^{\mathrm{3}} −{s}−{c} \\ $$$${let}\:\:{s}={p}+{m}\:\:\Rightarrow \\ $$$${p}^{\mathrm{3}} +\mathrm{3}{mp}^{\mathrm{2}} +\mathrm{3}{m}^{\mathrm{2}} {p}+{m}^{\mathrm{3}} −{p}−{m}−{c}−{k} \\ $$$$\:−{p}^{\mathrm{2}} −\mathrm{2}{mp}−{m}^{\mathrm{2}} +\mathrm{2}{hp}+\mathrm{2}{mh}−{h}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\underset{−} {{let}\:\:\mathrm{3}{m}=\mathrm{1}}\:\:\Rightarrow \\ $$$${p}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}\right)−\frac{\mathrm{8}}{\mathrm{27}}−{k}−\left({h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:{p}=\frac{\left({h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +{k}+\frac{\mathrm{8}}{\mathrm{27}}}{\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${but}\:\:\:{p}^{\mathrm{3}} ={p}+{c}\:\:\:\Rightarrow \\ $$$$\left\{\left({h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +{k}+\frac{\mathrm{8}}{\mathrm{27}}\right\}^{\mathrm{3}} \\ $$$$\:\:=\left\{\left({h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +{k}+\frac{\mathrm{8}}{\mathrm{27}}\right\}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:+{c}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$${let}\:\:{k}=\frac{\mathrm{2}{h}}{\mathrm{3}} \\ $$$$\:\:\left({h}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{27}}\right)^{\mathrm{3}} =\left({h}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{27}}\right)\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{c}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\:\left({h}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{27}}\right)\left({h}^{\mathrm{4}} +\frac{\mathrm{22}{h}^{\mathrm{2}} }{\mathrm{27}}+\frac{\mathrm{121}}{\mathrm{729}}−\mathrm{4}{h}^{\mathrm{2}} +\frac{\mathrm{4}{h}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{9}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={c}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$….. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *