Question-60045

Facebook Tweet Pin

Question Number 60045 by Kunal12588 last updated on 17/May/19

Commented by Kunal12588 last updated on 17/May/19

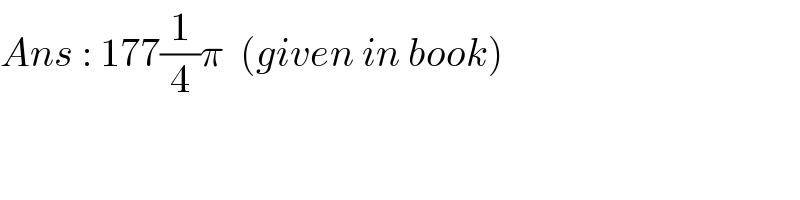
$${Ans}\::\:\mathrm{177}\frac{\mathrm{1}}{\mathrm{4}}\pi\:\:\left({given}\:{in}\:{book}\right) \\ $$

Commented by mr W last updated on 17/May/19

$${correct}! \\ $$

Answered by mr W last updated on 17/May/19

Commented by mr W last updated on 17/May/19

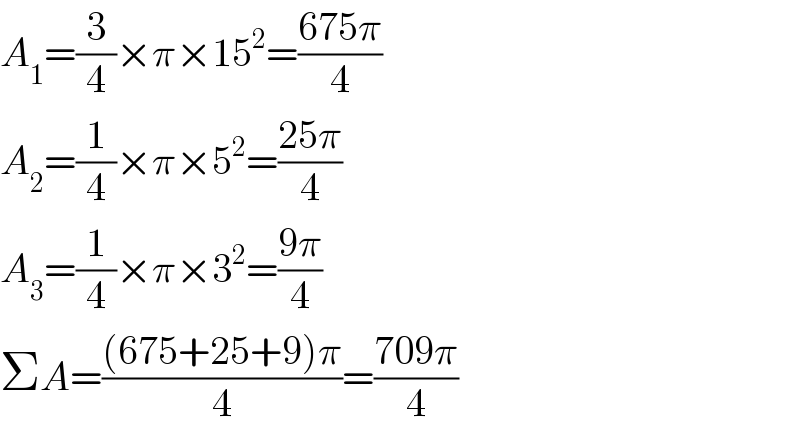
A_1 =(3/4)×π×15^2 =((675π)/4) A_2 =(1/4)×π×5^2 =((25π)/4) A_3 =(1/4)×π×3^2 =((9π)/4) ΣA=(((675+25+9)π)/4)=((709π)/4)

$${A}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{4}}×\pi×\mathrm{15}^{\mathrm{2}} =\frac{\mathrm{675}\pi}{\mathrm{4}} \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}×\pi×\mathrm{5}^{\mathrm{2}} =\frac{\mathrm{25}\pi}{\mathrm{4}} \\ $$$${A}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{4}}×\pi×\mathrm{3}^{\mathrm{2}} =\frac{\mathrm{9}\pi}{\mathrm{4}} \\ $$$$\Sigma{A}=\frac{\left(\mathrm{675}+\mathrm{25}+\mathrm{9}\right)\pi}{\mathrm{4}}=\frac{\mathrm{709}\pi}{\mathrm{4}} \\ $$

Commented by Kunal12588 last updated on 17/May/19