Question Number 60095 by Kunal12588 last updated on 17/May/19
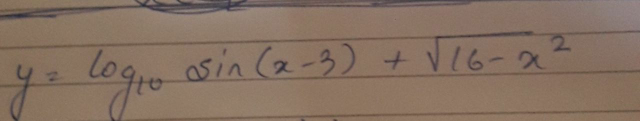
Commented by Kunal12588 last updated on 17/May/19

$${find}\:{Domain} \\ $$
Answered by tanmay last updated on 17/May/19
![log_(10) sin(x−3)+(√(16−x^2 )) g(x)=16−x^2 g(x)=(4+x)(4−x) g(x)=0 [[when x=−4 and x=4 g(x)<0 when x>4 g(x)<0 when x<−4 g(x)>0 when 4>x>−4 so for (√(16−x^2 )) 4≥x≥−4→x∈[−4,4] log_(10) sin(x−3) sin(x−3)>0 so when (x−3)>0 sin(x−3)>0 so log_(10) sin(x−3) fesible when x>3 x∈ (3,∞) so combining x∈ [−4,4]∩ (3,∞)→x∈(3,4]](https://www.tinkutara.com/question/Q60105.png)
$${log}_{\mathrm{10}} {sin}\left({x}−\mathrm{3}\right)+\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }\: \\ $$$${g}\left({x}\right)=\mathrm{16}−{x}^{\mathrm{2}} \\ $$$${g}\left({x}\right)=\left(\mathrm{4}+{x}\right)\left(\mathrm{4}−{x}\right) \\ $$$${g}\left({x}\right)=\mathrm{0}\:\:\:\:\left[\left[{when}\:{x}=−\mathrm{4}\:{and}\:{x}=\mathrm{4}\right.\right. \\ $$$${g}\left({x}\right)<\mathrm{0}\:\:\:{when}\:{x}>\mathrm{4} \\ $$$${g}\left({x}\right)<\mathrm{0}\:\:{when}\:{x}<−\mathrm{4} \\ $$$${g}\left({x}\right)>\mathrm{0}\:\:{when}\:\mathrm{4}>{x}>−\mathrm{4} \\ $$$${so}\:{for}\:\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }\:\:\:\mathrm{4}\geqslant{x}\geqslant−\mathrm{4}\rightarrow{x}\in\left[−\mathrm{4},\mathrm{4}\right] \\ $$$$ \\ $$$${log}_{\mathrm{10}} {sin}\left({x}−\mathrm{3}\right) \\ $$$${sin}\left({x}−\mathrm{3}\right)>\mathrm{0} \\ $$$${so}\:{when}\:\left({x}−\mathrm{3}\right)>\mathrm{0}\:\:\:\:{sin}\left({x}−\mathrm{3}\right)>\mathrm{0} \\ $$$$ \\ $$$${so}\:{log}_{\mathrm{10}} {sin}\left({x}−\mathrm{3}\right)\:{fesible}\:{when}\:{x}>\mathrm{3}\:{x}\in\:\left(\mathrm{3},\infty\right) \\ $$$${so}\:{combining} \\ $$$${x}\in\:\left[−\mathrm{4},\mathrm{4}\right]\cap\:\left(\mathrm{3},\infty\right)\rightarrow{x}\in\left(\mathrm{3},\mathrm{4}\right] \\ $$$$ \\ $$
