Question Number 125669 by mathocean1 last updated on 12/Dec/20
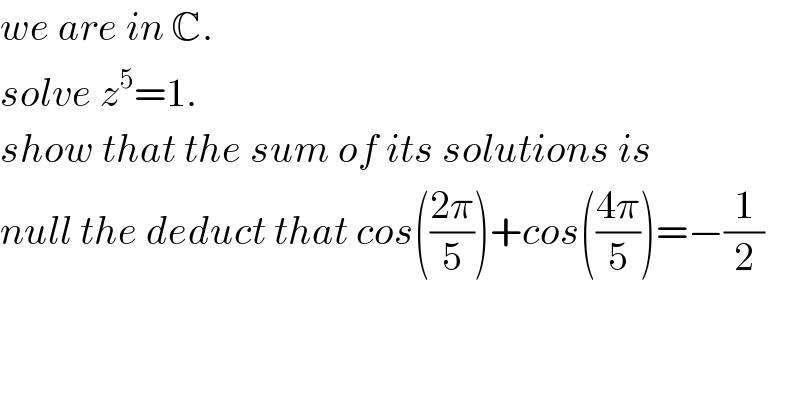
$${we}\:{are}\:{in}\:\mathbb{C}. \\ $$$${solve}\:{z}^{\mathrm{5}} =\mathrm{1}. \\ $$$${show}\:{that}\:{the}\:{sum}\:{of}\:{its}\:{solutions}\:{is} \\ $$$${null}\:{the}\:{deduct}\:{that}\:{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right)+{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 13/Dec/20

$${z}^{\mathrm{5}} +\mathrm{0}{z}^{\mathrm{4}} −\mathrm{1}=\mathrm{0} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}{z}_{{k}} =\mathrm{0}. \\ $$$${z}_{{k}} =\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{\mathrm{5}}+{i}\:\mathrm{sin}\:\frac{\mathrm{2}{k}\pi}{\mathrm{5}} \\ $$$$\Sigma{z}_{{k}} =\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{8}\pi}{\mathrm{5}}\right)+{i}\:\left(\mathrm{9}+\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{sin}\:\frac{\mathrm{6}\pi}{\mathrm{5}}+\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{8}\pi}{\mathrm{5}}=\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\left(\mathrm{2}\pi−\frac{\mathrm{4}\pi}{\mathrm{5}}\right)+\mathrm{cos}\:\left(\mathrm{2}\pi−\frac{\mathrm{2}\pi}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}=\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
