Menu Close

Question-125709

Tinku Tara 0 Comments
Pin




Question Number 125709 by mr W last updated on 13/Dec/20
Commented by mr W last updated on 13/Dec/20
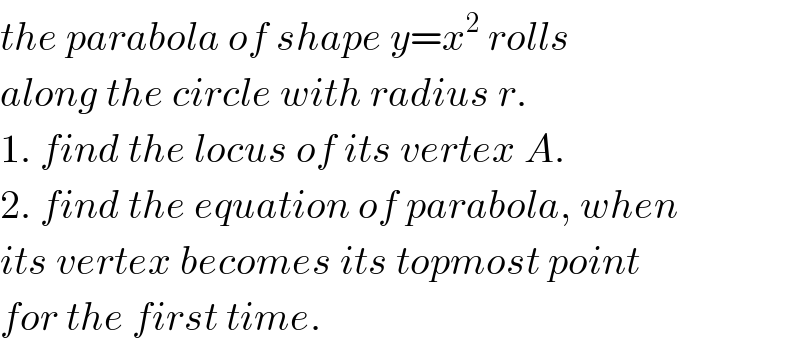
the parabola of shape y=x^2 rolls along the circle with radius r. 1. find the locus of its vertex A. 2. find the equation of parabola, when its vertex becomes its topmost point for the first time.
$${the}\:{parabola}\:{of}\:{shape}\:{y}={x}^{\mathrm{2}} \:{rolls} \\ $$$${along}\:{the}\:{circle}\:{with}\:{radius}\:{r}.\: \\ $$$$\mathrm{1}.\:{find}\:{the}\:{locus}\:{of}\:{its}\:{vertex}\:{A}. \\ $$$$\mathrm{2}.\:{find}\:{the}\:{equation}\:{of}\:{parabola},\:{when} \\ $$$${its}\:{vertex}\:{becomes}\:{its}\:{topmost}\:{point} \\ $$$${for}\:{the}\:{first}\:{time}. \\ $$
Answered by ajfour last updated on 13/Dec/20
Commented by ajfour last updated on 13/Dec/20
Contact point T(p, p^2 ) (with vertex of parabola as origin) tan φ=2p s=rθ=∫_0 ^( p) (√(1+4p^2 ))dp =(1/4){2p(√(1+4p^2 ))+ln (2p+(√(1+4p^2 )))} ⇒ 4rθ=sec φtan φ +ln (tan φ+sec φ) O(p+rsin φ, p^2 −rcos φ)≡(h,k) δ=θ+φ−(π/2) eq. of y axis in pq or XY coordinate Y−(p^2 −rcos φ) =tan δ{X−(p+rsin φ)} Y intercept (X=0) Y=p^2 −rcos φ−(p+rsin φ)tan δ x=−Ycos δ x=(p+rsin φ)sin δ −(p^2 −rcos φ)cos δ y=(k/(sin δ))+(x/(tan δ)) y=(((p^2 −rcos φ)/(sin δ)))+(p+rsin φ)cos δ −(((p^2 −rcos φ)/(sin δ)))cos^2 δ _________________________ y=(p+rsin φ)cos δ+(p^2 −rcos φ)sin δ x=(p+rsin φ)sin δ−(p^2 −rcos φ)cos δ 2p=tan φ δ=θ+φ−(π/2) 4rθ=sec φtan φ+ln (tan φ+sec φ) _________________________ when vetex of parabola becomes topmost point the first time in xy plane then θ+φ=π ⇒ δ=(π/2) y=p^2 −rcos φ x=p+rsin φ 2p=tan φ
$${Contact}\:{point}\:{T}\left({p},\:{p}^{\mathrm{2}} \right) \\ $$$$\left({with}\:{vertex}\:{of}\:{parabola}\:{as}\:{origin}\right) \\ $$$$\mathrm{tan}\:\phi=\mathrm{2}{p} \\ $$$${s}={r}\theta=\int_{\mathrm{0}} ^{\:{p}} \sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }{dp} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{2}{p}\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }+\mathrm{ln}\:\left(\mathrm{2}{p}+\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }\right)\right\} \\ $$$$\Rightarrow\:\mathrm{4}{r}\theta=\mathrm{sec}\:\phi\mathrm{tan}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{ln}\:\left(\mathrm{tan}\:\phi+\mathrm{sec}\:\phi\right) \\ $$$${O}\left({p}+{r}\mathrm{sin}\:\phi,\:{p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi\right)\equiv\left({h},{k}\right) \\ $$$$\delta=\theta+\phi−\frac{\pi}{\mathrm{2}} \\ $$$${eq}.\:{of}\:{y}\:{axis}\:{in}\:{pq}\:{or}\:{XY}\:{coordinate} \\ $$$${Y}−\left({p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi\right) \\ $$$$\:\:=\mathrm{tan}\:\delta\left\{{X}−\left({p}+{r}\mathrm{sin}\:\phi\right)\right\} \\ $$$${Y}\:{intercept}\:\:\left({X}=\mathrm{0}\right) \\ $$$${Y}={p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi−\left({p}+{r}\mathrm{sin}\:\phi\right)\mathrm{tan}\:\delta \\ $$$${x}=−{Y}\mathrm{cos}\:\delta \\ $$$${x}=\left({p}+{r}\mathrm{sin}\:\phi\right)\mathrm{sin}\:\delta \\ $$$$\:\:\:\:\:\:\:−\left({p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi\right)\mathrm{cos}\:\delta \\ $$$${y}=\frac{{k}}{\mathrm{sin}\:\delta}+\frac{{x}}{\mathrm{tan}\:\delta} \\ $$$${y}=\left(\frac{{p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi}{\mathrm{sin}\:\delta}\right)+\left({p}+{r}\mathrm{sin}\:\phi\right)\mathrm{cos}\:\delta \\ $$$$\:\:\:\:\:\:\:\:\:−\left(\frac{{p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi}{\mathrm{sin}\:\delta}\right)\mathrm{cos}\:^{\mathrm{2}} \delta \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${y}=\left({p}+{r}\mathrm{sin}\:\phi\right)\mathrm{cos}\:\delta+\left({p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi\right)\mathrm{sin}\:\delta \\ $$$${x}=\left({p}+{r}\mathrm{sin}\:\phi\right)\mathrm{sin}\:\delta−\left({p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi\right)\mathrm{cos}\:\delta \\ $$$$\mathrm{2}{p}=\mathrm{tan}\:\phi \\ $$$$\delta=\theta+\phi−\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{4}{r}\theta=\mathrm{sec}\:\phi\mathrm{tan}\:\phi+\mathrm{ln}\:\left(\mathrm{tan}\:\phi+\mathrm{sec}\:\phi\right) \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${when}\:{vetex}\:{of}\:{parabola}\:{becomes} \\ $$$${topmost}\:{point}\:{the}\:{first}\:{time}\:{in} \\ $$$${xy}\:{plane}\:{then}\:\:\theta+\phi=\pi \\ $$$$\Rightarrow\:\:\delta=\frac{\pi}{\mathrm{2}} \\ $$$${y}={p}^{\mathrm{2}} −{r}\mathrm{cos}\:\phi \\ $$$${x}={p}+{r}\mathrm{sin}\:\phi \\ $$$$\mathrm{2}{p}=\mathrm{tan}\:\phi \\ $$
Commented by mr W last updated on 13/Dec/20
perfect! your approach is very smart.
$${perfect}!\:{your}\:{approach}\:{is}\:{very}\:{smart}. \\ $$
Commented by ajfour last updated on 13/Dec/20
i shall have to edit, sir. I tried plotting, it dint come out correct on grapher...
Commented by mr W last updated on 13/Dec/20
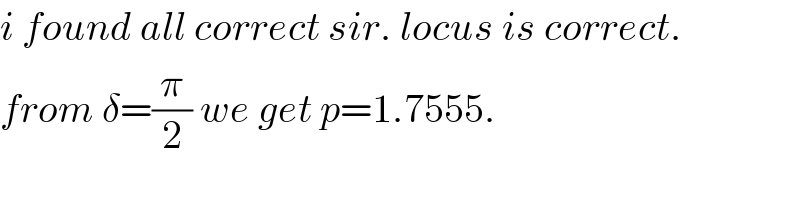
i found all correct sir. locus is correct. from δ=(π/2) we get p=1.7555.
$${i}\:{found}\:{all}\:{correct}\:{sir}.\:{locus}\:{is}\:{correct}. \\ $$$${from}\:\delta=\frac{\pi}{\mathrm{2}}\:{we}\:{get}\:{p}=\mathrm{1}.\mathrm{7555}. \\ $$
Commented by mr W last updated on 13/Dec/20
Answered by mr W last updated on 13/Dec/20
Commented by mr W last updated on 13/Dec/20
P(t,t^2 ) in x′y′−system AP_(Parabola) =(1/4)[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] AP_(Circle) =rϕ ⇒ϕ=(1/(4r))[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] tan θ=2t sin θ=((2t)/( (√(1+4t^2 )))) cos θ=(1/( (√(1+4t^2 )))) P(r sin ϕ, r cos ϕ) in xy−system φ=θ+ϕ−(π/2) x_A =r sin ϕ+t sin φ−(t^2 −f)cos φ =r sin ϕ−t cos (θ+ϕ) −(t^2 −f)sin (θ+ϕ) =r sin ϕ−t cos θ cos ϕ+t sin θ sin ϕ −(t^2 −f)sin θ cos ϕ−(t^2 −f)cos θ sin ϕ =r sin ϕ−cos θ [(t^2 −f) sin ϕ+t cos ϕ]+sin θ[t sin ϕ −(t^2 −f)cos ϕ] =r sin ϕ−(1/( (√(1+4t^2 )))) [(t^2 −f) sin ϕ+t cos ϕ]+((2t)/( (√(1+4t^2 ))))[t sin ϕ −(t^2 −f)cos ϕ] y_A =r cos ϕ+t cos φ+(t^2 −f)sin φ =r cos ϕ+t sin (θ+ϕ)−(t^2 −f)cos (θ+ϕ) =r cos ϕ+t sin θ cos ϕ+t cos θ sin ϕ−(t^2 −f)cos θ cos ϕ+(t^2 −f)sin θ sin ϕ =r cos ϕ+ cos θ[t sin ϕ−(t^2 −f) cos ϕ]+sin θ[(t^2 −f)sin ϕ+t cos ϕ] =r cos ϕ+ (1/( (√(1+4t^2 ))))[t sin ϕ−(t^2 −f) cos ϕ]+((2t)/( (√(1+4t^2 ))))[(t^2 −f)sin ϕ+t cos ϕ] A: { ((x=r sin ϕ−(1/( (√(1+4t^2 )))) [(t^2 −f) sin ϕ+t cos ϕ]+((2t)/( (√(1+4t^2 ))))[t sin ϕ −(t^2 −f)cos ϕ])),((y=r cos ϕ+ (1/( (√(1+4t^2 ))))[t sin ϕ−(t^2 −f) cos ϕ]+((2t)/( (√(1+4t^2 ))))[(t^2 −f)sin ϕ+t cos ϕ])) :} (offset f is introduced here to treat a different point other than the vertex) when A is topmost in xy−system: φ=(π/2) θ+ϕ=π tan^(−1) (2t)+(1/(4r))[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))]=π ⇒t≈1.7556
$${P}\left({t},{t}^{\mathrm{2}} \right)\:{in}\:{x}'{y}'−{system} \\ $$$${AP}_{{Parabola}} =\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$${AP}_{{Circle}} ={r}\varphi \\ $$$$\Rightarrow\varphi=\frac{\mathrm{1}}{\mathrm{4}{r}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{t} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }} \\ $$$$ \\ $$$${P}\left({r}\:\mathrm{sin}\:\varphi,\:{r}\:\mathrm{cos}\:\varphi\right)\:{in}\:{xy}−{system} \\ $$$$\phi=\theta+\varphi−\frac{\pi}{\mathrm{2}} \\ $$$${x}_{{A}} ={r}\:\mathrm{sin}\:\varphi+{t}\:\mathrm{sin}\:\phi−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\phi \\ $$$$={r}\:\mathrm{sin}\:\varphi−{t}\:\mathrm{cos}\:\left(\theta+\varphi\right)\:−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\left(\theta+\varphi\right) \\ $$$$={r}\:\mathrm{sin}\:\varphi−{t}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi+{t}\:\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi\:−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$={r}\:\mathrm{sin}\:\varphi−\mathrm{cos}\:\theta\:\left[\left({t}^{\mathrm{2}} −{f}\right)\:\mathrm{sin}\:\varphi+{t}\:\mathrm{cos}\:\varphi\right]+\mathrm{sin}\:\theta\left[{t}\:\mathrm{sin}\:\varphi\:−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\varphi\right] \\ $$$$={r}\:\mathrm{sin}\:\varphi−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\:\left[\left({t}^{\mathrm{2}} −{f}\right)\:\mathrm{sin}\:\varphi+{t}\:\mathrm{cos}\:\varphi\right]+\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left[{t}\:\mathrm{sin}\:\varphi\:−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\varphi\right] \\ $$$$ \\ $$$${y}_{{A}} ={r}\:\mathrm{cos}\:\varphi+{t}\:\mathrm{cos}\:\phi+\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\phi \\ $$$$={r}\:\mathrm{cos}\:\varphi+{t}\:\mathrm{sin}\:\left(\theta+\varphi\right)−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\left(\theta+\varphi\right) \\ $$$$={r}\:\mathrm{cos}\:\varphi+{t}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi+{t}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi+\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$={r}\:\mathrm{cos}\:\varphi+\:\mathrm{cos}\:\theta\left[{t}\:\mathrm{sin}\:\varphi−\left({t}^{\mathrm{2}} −{f}\right)\:\mathrm{cos}\:\varphi\right]+\mathrm{sin}\:\theta\left[\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\varphi+{t}\:\mathrm{cos}\:\varphi\right] \\ $$$$={r}\:\mathrm{cos}\:\varphi+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left[{t}\:\mathrm{sin}\:\varphi−\left({t}^{\mathrm{2}} −{f}\right)\:\mathrm{cos}\:\varphi\right]+\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left[\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\varphi+{t}\:\mathrm{cos}\:\varphi\right] \\ $$$${A}:\begin{cases}{{x}={r}\:\mathrm{sin}\:\varphi−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\:\left[\left({t}^{\mathrm{2}} −{f}\right)\:\mathrm{sin}\:\varphi+{t}\:\mathrm{cos}\:\varphi\right]+\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left[{t}\:\mathrm{sin}\:\varphi\:−\left({t}^{\mathrm{2}} −{f}\right)\mathrm{cos}\:\varphi\right]}\\{{y}={r}\:\mathrm{cos}\:\varphi+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left[{t}\:\mathrm{sin}\:\varphi−\left({t}^{\mathrm{2}} −{f}\right)\:\mathrm{cos}\:\varphi\right]+\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left[\left({t}^{\mathrm{2}} −{f}\right)\mathrm{sin}\:\varphi+{t}\:\mathrm{cos}\:\varphi\right]}\end{cases} \\ $$$$\left({offset}\:{f}\:{is}\:{introduced}\:{here}\:{to}\:{treat}\:{a}\right. \\ $$$$\left.{different}\:{point}\:{other}\:{than}\:{the}\:{vertex}\right) \\ $$$$ \\ $$$${when}\:{A}\:{is}\:{topmost}\:{in}\:{xy}−{system}: \\ $$$$\phi=\frac{\pi}{\mathrm{2}} \\ $$$$\theta+\varphi=\pi \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{t}\right)+\frac{\mathrm{1}}{\mathrm{4}{r}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right]=\pi \\ $$$$\Rightarrow{t}\approx\mathrm{1}.\mathrm{7556} \\ $$
Commented by mr W last updated on 13/Dec/20
Commented by ajfour last updated on 13/Dec/20
Sir, can you try and help plotting my graph for the second part of the question? i dont get it correct, neither can find mistake in my solution..
$${Sir},\:{can}\:{you}\:{try}\:{and}\:{help}\:{plotting} \\ $$$${my}\:{graph}\:{for}\:{the}\:{second}\:{part}\:{of} \\ $$$${the}\:{question}?\:{i}\:{dont}\:{get}\:{it}\:{correct}, \\ $$$${neither}\:{can}\:{find}\:{mistake}\:{in}\:{my} \\ $$$${solution}.. \\ $$
Commented by mr W last updated on 13/Dec/20
i found no mistake in your solution. all is correct.
$${i}\:{found}\:{no}\:{mistake}\:{in}\:{your}\:{solution}. \\ $$$${all}\:{is}\:{correct}. \\ $$
Commented by ajfour last updated on 13/Dec/20
Thanks enormously Sir, I just then need to learn plotting on grapher the parametric way!
$${Thanks}\:{enormously}\:{Sir},\:{I}\:{just} \\ $$$${then}\:{need}\:{to}\:{learn}\:{plotting} \\ $$$${on}\:{grapher}\:{the}\:{parametric}\:{way}! \\ $$
Commented by mr W last updated on 15/Dec/20
great to see you again too!
$${great}\:{to}\:{see}\:{you}\:{again}\:{too}! \\ $$
Commented by Tinkutara last updated on 15/Dec/20
Great to see you both mrW and ajfour Sirs active still!
Commented by ajfour last updated on 15/Dec/20
how well are you doing at college, engineering mathematics?
$${how}\:{well}\:{are}\:{you}\:{doing}\:{at}\:{college}, \\ $$$${engineering}\:{mathematics}? \\ $$
Commented by Tinkutara last updated on 16/Dec/20
I am doing Civil Engg from prestigious IIT.! Thanks for your support Sir!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *