Question Number 125728 by Mammadli last updated on 13/Dec/20
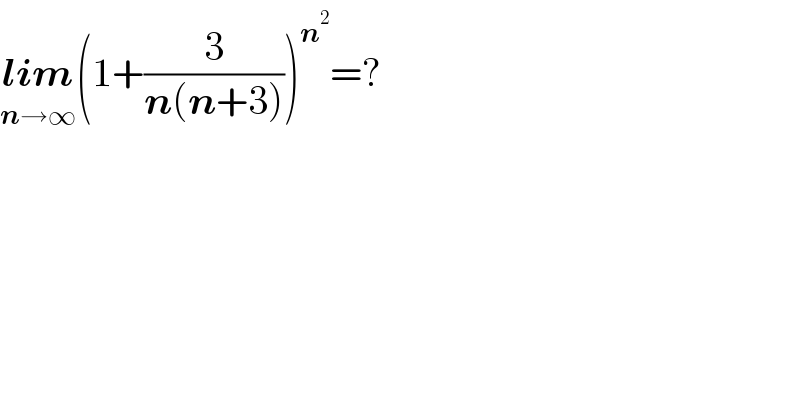
$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{lim}}}\left(\mathrm{1}+\frac{\mathrm{3}}{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{3}\right)}\right)^{\boldsymbol{{n}}^{\mathrm{2}} } =? \\ $$
Answered by bramlexs22 last updated on 13/Dec/20
![lim_(x→∞) [(1+(3/(n^2 +3n)))^((n^2 +3n)/3) ]^((3n^2 )/(n^2 +3n)) = e^(lim_(x→∞) (((3n^2 )/(n^2 +3n)))) = e^3](https://www.tinkutara.com/question/Q125729.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\left(\mathrm{1}+\frac{\mathrm{3}}{{n}^{\mathrm{2}} +\mathrm{3}{n}}\right)^{\frac{{n}^{\mathrm{2}} +\mathrm{3}{n}}{\mathrm{3}}} \right]^{\frac{\mathrm{3}{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} +\mathrm{3}{n}}} \\ $$$$=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} +\mathrm{3}{n}}\right)} \:=\:{e}^{\mathrm{3}} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Dec/20
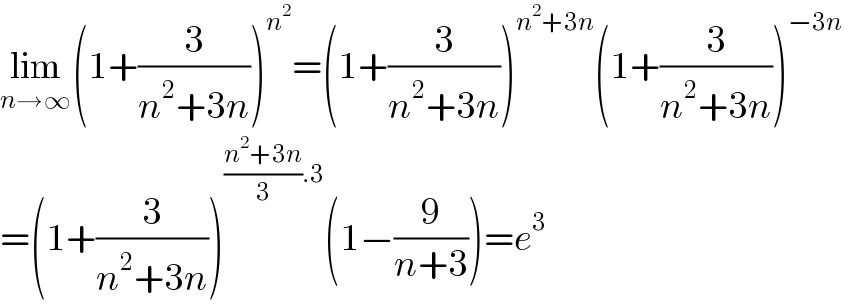
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}^{\mathrm{2}} +\mathrm{3}{n}}\right)^{{n}^{\mathrm{2}} } =\left(\mathrm{1}+\frac{\mathrm{3}}{{n}^{\mathrm{2}} +\mathrm{3}{n}}\right)^{{n}^{\mathrm{2}} +\mathrm{3}{n}} \left(\mathrm{1}+\frac{\mathrm{3}}{{n}^{\mathrm{2}} +\mathrm{3}{n}}\right)^{−\mathrm{3}{n}} \: \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{3}}{{n}^{\mathrm{2}} +\mathrm{3}{n}}\right)^{\frac{{n}^{\mathrm{2}} +\mathrm{3}{n}}{\mathrm{3}}.\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{9}}{{n}+\mathrm{3}}\right)={e}^{\mathrm{3}} \\ $$
