Menu Close

dx-tan-4-x-1-

Tinku Tara 0 Comments
Pin




Question Number 125895 by john_santu last updated on 15/Dec/20
∫ (dx/(tan^4 x+1)) ?
$$\:\:\:\:\int\:\frac{{dx}}{\mathrm{tan}\:^{\mathrm{4}} {x}+\mathrm{1}}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 15/Dec/20
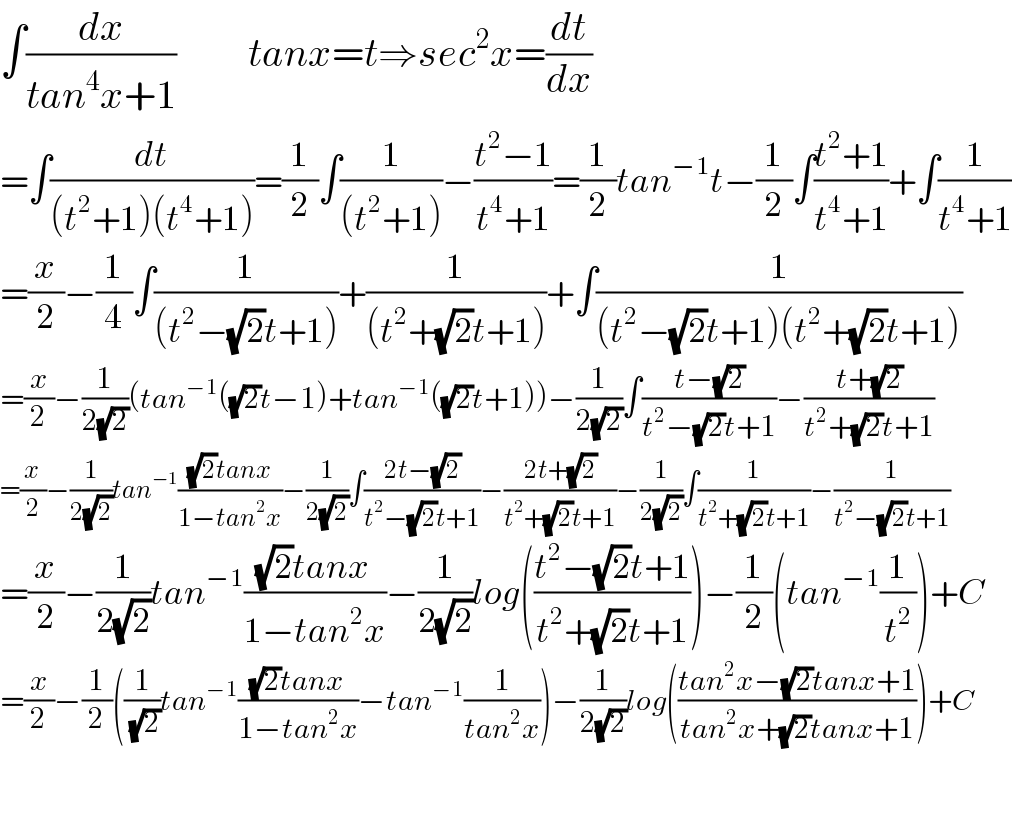
∫(dx/(tan^4 x+1)) tanx=t⇒sec^2 x=(dt/dx) =∫(dt/((t^2 +1)(t^4 +1)))=(1/2)∫(1/((t^2 +1)))−((t^2 −1)/(t^4 +1))=(1/2)tan^(−1) t−(1/2)∫((t^2 +1)/(t^4 +1))+∫(1/(t^4 +1)) =(x/2)−(1/4)∫(1/((t^2 −(√2)t+1)))+(1/((t^2 +(√2)t+1)))+∫(1/((t^2 −(√2)t+1)(t^2 +(√2)t+1))) =(x/2)−(1/(2(√2)))(tan^(−1) ((√2)t−1)+tan^(−1) ((√2)t+1))−(1/(2(√2)))∫((t−(√2))/(t^2 −(√2)t+1))−((t+(√2))/(t^2 +(√2)t+1)) =(x/2)−(1/(2(√2)))tan^(−1) (((√2)tanx)/(1−tan^2 x))−(1/(2(√2)))∫((2t−(√2))/(t^2 −(√2)t+1))−((2t+(√2))/(t^2 +(√2)t+1))−(1/(2(√2)))∫(1/(t^2 +(√2)t+1))−(1/(t^2 −(√2)t+1)) =(x/2)−(1/(2(√2)))tan^(−1) (((√2)tanx)/(1−tan^2 x))−(1/(2(√2)))log(((t^2 −(√2)t+1)/(t^2 +(√2)t+1)))−(1/2)(tan^(−1) (1/t^2 ))+C =(x/2)−(1/2)((1/( (√2)))tan^(−1) (((√2)tanx)/(1−tan^2 x))−tan^(−1) (1/(tan^2 x)))−(1/(2(√2)))log(((tan^2 x−(√2)tanx+1)/(tan^2 x+(√2)tanx+1)))+C
$$\int\frac{{dx}}{{tan}^{\mathrm{4}} {x}+\mathrm{1}}\:\:\:\:\:\:\:\:\:{tanx}={t}\Rightarrow{sec}^{\mathrm{2}} {x}=\frac{{dt}}{{dx}} \\ $$$$=\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} {t}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}}+\int\frac{\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)}+\int\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)} \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left({tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)+{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{t}−\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}−\frac{{t}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}\: \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{\mathrm{2}{t}−\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}−\frac{\mathrm{2}{t}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}} \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)+{C} \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}−{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{tan}^{\mathrm{2}} {x}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{{tan}^{\mathrm{2}} {x}−\sqrt{\mathrm{2}}{tanx}+\mathrm{1}}{{tan}^{\mathrm{2}} {x}+\sqrt{\mathrm{2}}{tanx}+\mathrm{1}}\right)+{C} \\ $$$$ \\ $$
Commented by MJS_new last updated on 15/Dec/20
I get (just more transforming I guess) (x/2)+((√2)/8)(ln ∣(√2)+sin 2x∣ −ln ∣(√2)−sin 2x∣) +C
$$\mathrm{I}\:\mathrm{get}\:\left(\mathrm{just}\:\mathrm{more}\:\mathrm{transforming}\:\mathrm{I}\:\mathrm{guess}\right) \\ $$$$\frac{{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{ln}\:\mid\sqrt{\mathrm{2}}+\mathrm{sin}\:\mathrm{2}{x}\mid\:−\mathrm{ln}\:\mid\sqrt{\mathrm{2}}−\mathrm{sin}\:\mathrm{2}{x}\mid\right)\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *