Question Number 125968 by bramlexs22 last updated on 16/Dec/20
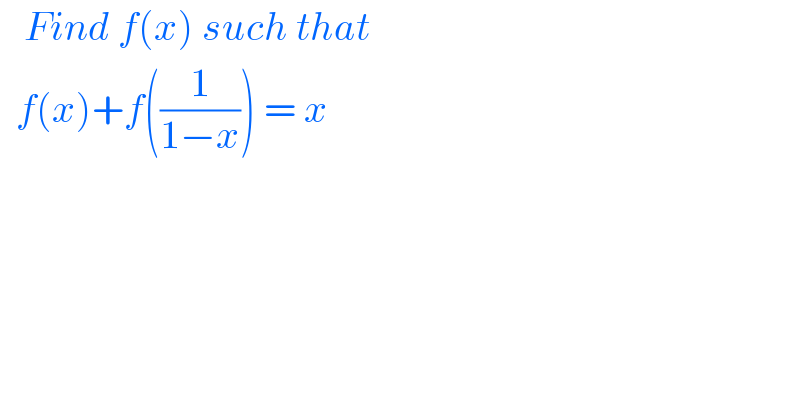
$$\:\:\:{Find}\:{f}\left({x}\right)\:{such}\:{that}\: \\ $$$$\:\:{f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)\:=\:{x} \\ $$
Answered by liberty last updated on 16/Dec/20
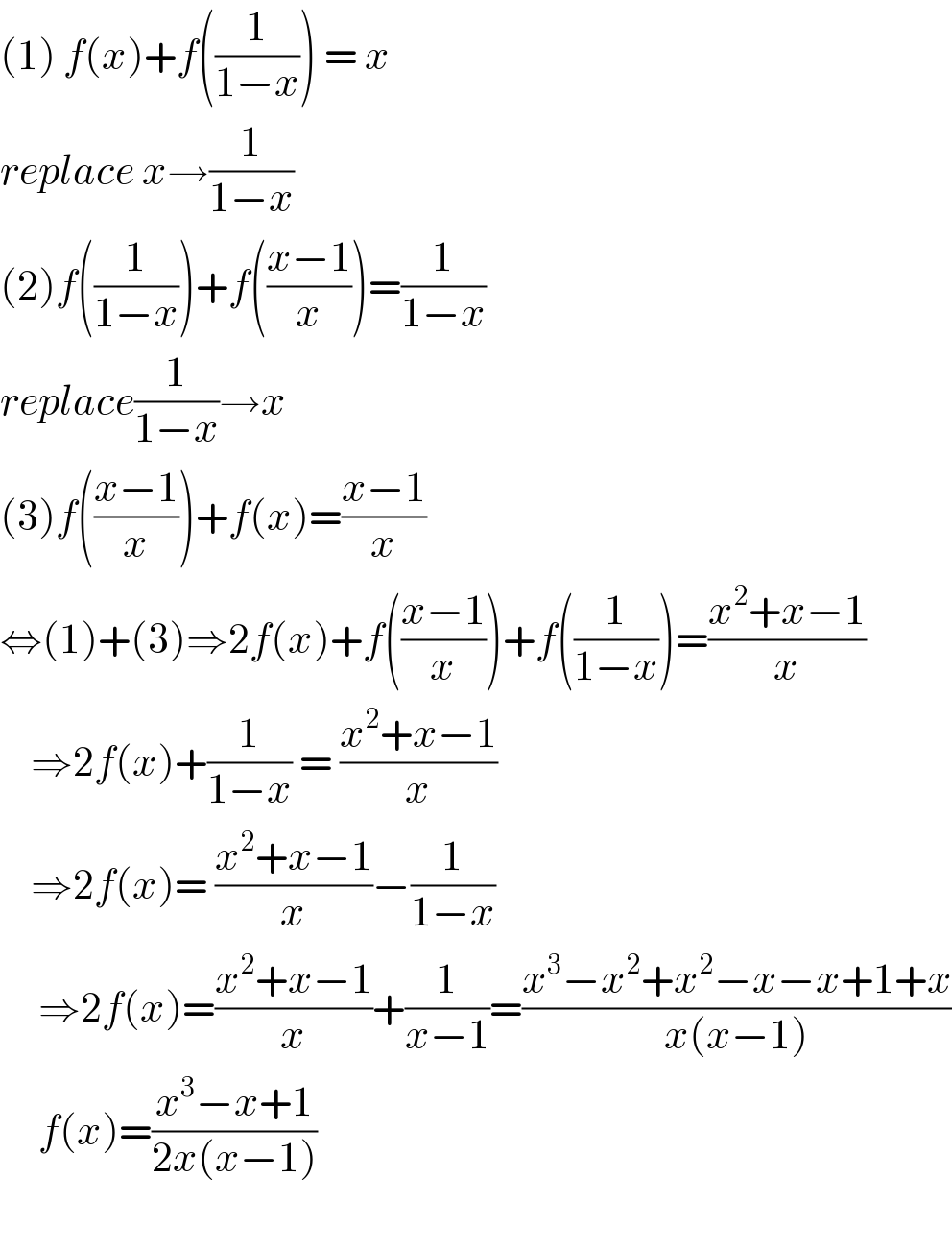
$$\left(\mathrm{1}\right)\:{f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)\:=\:{x} \\ $$$${replace}\:{x}\rightarrow\frac{\mathrm{1}}{\mathrm{1}−{x}}\: \\ $$$$\left(\mathrm{2}\right){f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${replace}\frac{\mathrm{1}}{\mathrm{1}−{x}}\rightarrow{x} \\ $$$$\left(\mathrm{3}\right){f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)+{f}\left({x}\right)=\frac{{x}−\mathrm{1}}{{x}} \\ $$$$\Leftrightarrow\left(\mathrm{1}\right)+\left(\mathrm{3}\right)\Rightarrow\mathrm{2}{f}\left({x}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)+{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)=\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\Rightarrow\mathrm{2}{f}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\Rightarrow\mathrm{2}{f}\left({x}\right)=\:\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{1}−{x}}\: \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{2}{f}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}−\mathrm{1}}=\frac{{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −{x}−{x}+\mathrm{1}+{x}}{{x}\left({x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:{f}\left({x}\right)=\frac{{x}^{\mathrm{3}} −{x}+\mathrm{1}}{\mathrm{2}{x}\left({x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\: \\ $$
