Question Number 71518 by TawaTawa last updated on 16/Oct/19

$$\mathrm{Express}\:\:\sqrt{\mathrm{28}}\:\:\mathrm{as}\:\mathrm{continued}\:\mathrm{fraction} \\ $$
Commented by Prithwish sen last updated on 16/Oct/19
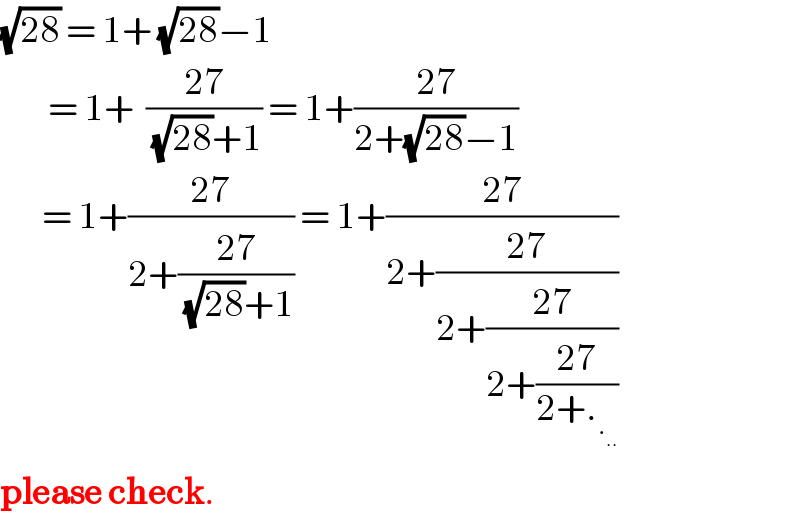
$$\sqrt{\mathrm{28}}\:=\:\mathrm{1}+\:\sqrt{\mathrm{28}}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{1}+\:\:\frac{\mathrm{27}}{\:\sqrt{\mathrm{28}}+\mathrm{1}}\:=\:\mathrm{1}+\frac{\mathrm{27}}{\mathrm{2}+\sqrt{\mathrm{28}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{1}+\frac{\mathrm{27}}{\mathrm{2}+\frac{\mathrm{27}}{\:\sqrt{\mathrm{28}}+\mathrm{1}}}\:=\:\mathrm{1}+\frac{\mathrm{27}}{\mathrm{2}+\frac{\mathrm{27}}{\mathrm{2}+\frac{\mathrm{27}}{\mathrm{2}+\frac{\mathrm{27}}{\mathrm{2}+._{._{..} } }}}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by Prithwish sen last updated on 16/Oct/19
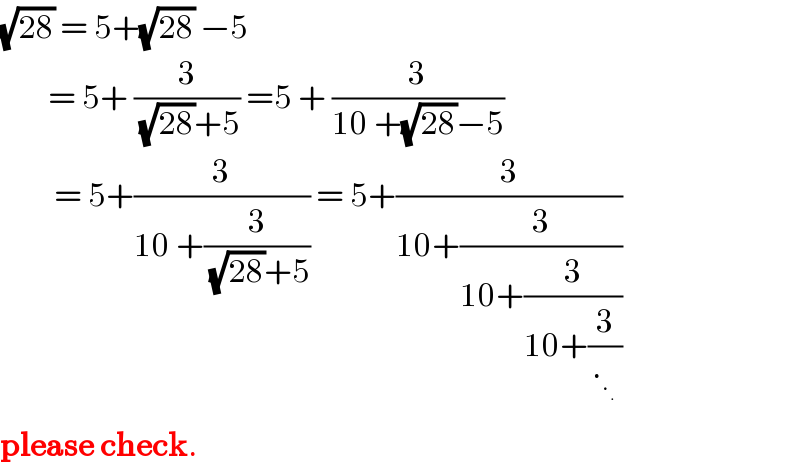
$$\sqrt{\mathrm{28}}\:=\:\mathrm{5}+\sqrt{\mathrm{28}}\:−\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{5}+\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{28}}+\mathrm{5}}\:=\mathrm{5}\:+\:\frac{\mathrm{3}}{\mathrm{10}\:+\sqrt{\mathrm{28}}−\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{5}+\frac{\mathrm{3}}{\mathrm{10}\:+\frac{\mathrm{3}}{\:\sqrt{\mathrm{28}}+\mathrm{5}}}\:=\:\mathrm{5}+\frac{\mathrm{3}}{\mathrm{10}+\frac{\mathrm{3}}{\mathrm{10}+\frac{\mathrm{3}}{\mathrm{10}+\frac{\mathrm{3}}{._{._{.} } }}}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by TawaTawa last updated on 16/Oct/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 16/Oct/19

Commented by TawaTawa last updated on 16/Oct/19
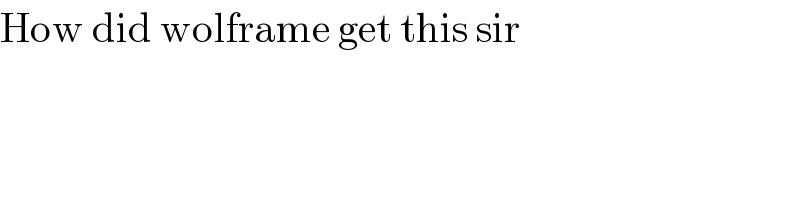
$$\mathrm{How}\:\mathrm{did}\:\mathrm{wolframe}\:\mathrm{get}\:\mathrm{this}\:\mathrm{sir} \\ $$
Commented by Prithwish sen last updated on 16/Oct/19

$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{back}}\:\boldsymbol{\mathrm{calculation}} \\ $$$$\boldsymbol{\mathrm{If}}\:\:\boldsymbol{\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{10}+\boldsymbol{\mathrm{x}}}}}} \\ $$$$\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{calculating}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{10}\boldsymbol{\mathrm{x}}−\mathrm{3}\:=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{\mathrm{x}}\:=\:−\mathrm{5}\pm\sqrt{\mathrm{28}} \\ $$$$\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{dont}}\:\boldsymbol{\mathrm{think}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{be}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{expression}}. \\ $$$$\boldsymbol{\mathrm{Please}}\:\boldsymbol{\mathrm{anyone}}\:\boldsymbol{\mathrm{give}}\:\boldsymbol{\mathrm{some}}\:\boldsymbol{\mathrm{comments}}. \\ $$
Commented by mr W last updated on 16/Oct/19
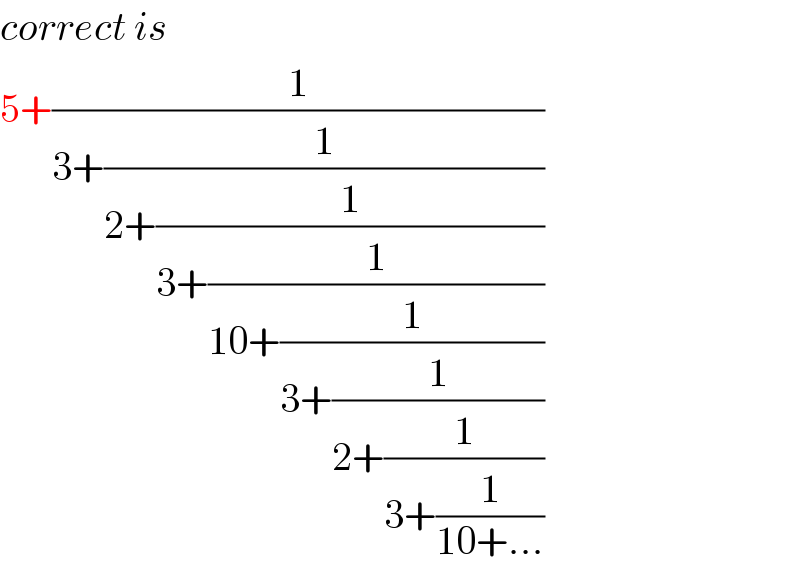
$${correct}\:{is} \\ $$$$\mathrm{5}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{10}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{10}+…}}}}}}}} \\ $$
Commented by Prithwish sen last updated on 17/Oct/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 16/Oct/19

$$\mathrm{5}<\sqrt{\mathrm{28}}<\mathrm{6} \\ $$$${x}_{\mathrm{0}} =\sqrt{\mathrm{28}},\:{a}_{\mathrm{0}} =\lfloor{x}_{\mathrm{0}} \rfloor=\mathrm{5} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{28}}−\mathrm{5}}=\frac{\sqrt{\mathrm{28}}+\mathrm{5}}{\mathrm{3}},\:{a}_{\mathrm{1}} =\lfloor{x}_{\mathrm{1}} \rfloor=\mathrm{3} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{28}}+\mathrm{5}}{\mathrm{3}}−\mathrm{3}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{28}}−\mathrm{4}}=\frac{\sqrt{\mathrm{28}}+\mathrm{4}}{\mathrm{4}},\:{a}_{\mathrm{2}} =\lfloor{x}_{\mathrm{2}} \rfloor=\mathrm{2} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{28}}+\mathrm{4}}{\mathrm{4}}−\mathrm{2}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{28}}−\mathrm{4}}=\frac{\sqrt{\mathrm{28}}+\mathrm{4}}{\mathrm{3}},\:{a}_{\mathrm{3}} =\lfloor{x}_{\mathrm{3}} \rfloor=\mathrm{3} \\ $$$${x}_{\mathrm{4}} =\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{28}}+\mathrm{4}}{\mathrm{3}}−\mathrm{3}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{28}}−\mathrm{5}}=\sqrt{\mathrm{28}}+\mathrm{5},\:{a}_{\mathrm{4}} =\lfloor{x}_{\mathrm{4}} \rfloor=\mathrm{10} \\ $$$${x}_{\mathrm{5}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{28}}+\mathrm{5}−\mathrm{10}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{28}}−\mathrm{5}}=\frac{\sqrt{\mathrm{28}}+\mathrm{5}}{\mathrm{3}}={x}_{\mathrm{1}} ,\:{a}_{\mathrm{4}} ={a}_{\mathrm{1}} =\mathrm{3} \\ $$$$…… \\ $$$$\Rightarrow\sqrt{\mathrm{28}}=\mathrm{5}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{10}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{10}+…}}}}}}}} \\ $$$$ \\ $$$${an}\:{other}\:{example}\:\sqrt{\mathrm{38}} \\ $$$$\mathrm{6}<\sqrt{\mathrm{38}}<\mathrm{7} \\ $$$${x}_{\mathrm{0}} =\sqrt{\mathrm{38}},\:{a}_{\mathrm{0}} =\lfloor{x}_{\mathrm{0}} \rfloor=\mathrm{6} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{38}}−\mathrm{6}}=\frac{\sqrt{\mathrm{38}}+\mathrm{6}}{\mathrm{2}},\:{a}_{\mathrm{1}} =\lfloor{x}_{\mathrm{1}} \rfloor=\mathrm{6} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{38}}+\mathrm{6}}{\mathrm{2}}−\mathrm{6}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{38}}−\mathrm{6}}=\sqrt{\mathrm{38}}+\mathrm{6},\:{a}_{\mathrm{2}} =\lfloor{x}_{\mathrm{2}} \rfloor=\mathrm{12} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{38}}+\mathrm{6}−\mathrm{12}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{38}}−\mathrm{6}}=\frac{\sqrt{\mathrm{38}}+\mathrm{6}}{\mathrm{2}}={x}_{\mathrm{1}} ,\:{a}_{\mathrm{3}} ={a}_{\mathrm{1}} =\mathrm{6} \\ $$$$…… \\ $$$$\Rightarrow\sqrt{\mathrm{38}}=\mathrm{6}+\frac{\mathrm{1}}{\mathrm{6}+\frac{\mathrm{1}}{\mathrm{12}+\frac{\mathrm{1}}{\mathrm{6}+\frac{\mathrm{1}}{\mathrm{12}+…}}}} \\ $$
Commented by TawaTawa last updated on 16/Oct/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 17/Oct/19

$$\mathrm{How}\:\mathrm{can}\:\mathrm{i}\:\mathrm{use}\:\mathrm{it}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{to}\:\:\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{28y}^{\mathrm{2}} \:\:=\:\:\mathrm{1} \\ $$
Commented by mind is power last updated on 17/Oct/19

$$\mathrm{X}^{\mathrm{2}} −\mathrm{28y}^{\mathrm{2}} =\mathrm{1}? \\ $$
Commented by TawaTawa last updated on 17/Oct/19

$$\mathrm{Yes}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 17/Oct/19

$${x}^{\mathrm{2}} −\mathrm{28}{y}^{\mathrm{2}} =\mathrm{1}\:{is}\:{a}\:{curve},\:{it}\:{has}\:{infinite} \\ $$$${solutions}\:\left({x},{y}\right).\:{this}\:{has}\:{nothing}\:{to}\:{do} \\ $$$${with}\:{how}\:{you}\:{express}\:\sqrt{\mathrm{28}}. \\ $$
Commented by Prithwish sen last updated on 17/Oct/19

$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{long}\:\mathrm{process}.\boldsymbol{\mathrm{Please}}\:\boldsymbol{\mathrm{see}}\:\boldsymbol{\mathrm{PELL}}'\boldsymbol{\mathrm{S}}\:\boldsymbol{\mathrm{equation}}. \\ $$$$\boldsymbol{\mathrm{Or}}\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{give}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{some}}\:\boldsymbol{\mathrm{time}}. \\ $$
Commented by Prithwish sen last updated on 17/Oct/19
![x^2 −28y^2 =1 now (√(28)) =[5, 3,2,3,10 ] the expression is periodic from 10 ∴ the first 4 convergents are (5/1),((16)/3),((37)/7),((127)/(24)) = (p_1 /q_1 ) thus the equation satisfies for x=127 and y=24 please check I have the solutions only .For further information you have to study the Pell′s equation.](https://www.tinkutara.com/question/Q71589.png)
$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{28}\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\mathrm{1} \\ $$$$\boldsymbol{\mathrm{now}}\:\sqrt{\mathrm{28}}\:=\left[\mathrm{5},\:\mathrm{3},\mathrm{2},\mathrm{3},\mathrm{10}\:\right] \\ $$$$\mathrm{the}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{periodic}\:\mathrm{from}\:\mathrm{10} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{first}\:\mathrm{4}\:\mathrm{convergents}\:\mathrm{are} \\ $$$$\frac{\mathrm{5}}{\mathrm{1}},\frac{\mathrm{16}}{\mathrm{3}},\frac{\mathrm{37}}{\mathrm{7}},\frac{\mathrm{127}}{\mathrm{24}}\:=\:\frac{\boldsymbol{\mathrm{p}}_{\mathrm{1}} }{\boldsymbol{\mathrm{q}}_{\mathrm{1}} } \\ $$$$\boldsymbol{\mathrm{thus}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equation}}\:\boldsymbol{\mathrm{satisfies}}\:\boldsymbol{\mathrm{for}} \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{127}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{y}}=\mathrm{24} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$$$\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{solutions}}\:\boldsymbol{\mathrm{only}}\:.\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{further}}\:\boldsymbol{\mathrm{information}} \\ $$$$\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{study}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{Pell}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{equation}}. \\ $$
Commented by TawaTawa last updated on 17/Oct/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
