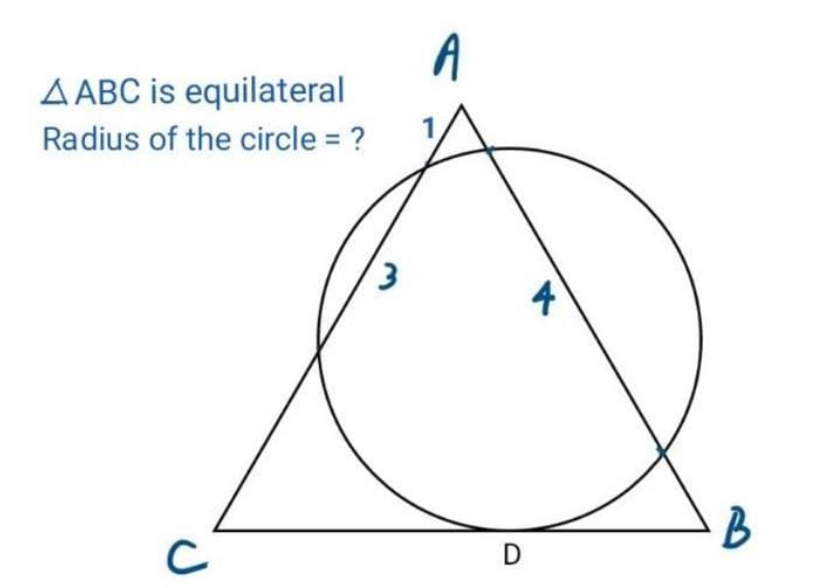
Question Number 191714 by Mingma last updated on 29/Apr/23
Commented by AST last updated on 29/Apr/23

Answered by AST last updated on 29/Apr/23

$${Let}\:{AC}\:{intersect}\:{the}\:{circle}\:{from}\:{A} \\ $$$${at}\:{E}\:{and}\:{F}\:{respectively}\: \\ $$$${Let}\:{AB}\:{also}\:{intersect}\:{the}\:{circle}\:{from} \\ $$$${A}\:{at}\:{X}\:{and}\:{Y}\:{respectively}. \\ $$$${Power}\:{of}\:{point}\Rightarrow{AE}×{AF}={AX}×{AY} \\ $$$$\Rightarrow\mathrm{1}×\mathrm{4}={AX}\left({AX}+\mathrm{4}\right)\Rightarrow{AX}=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2} \\ $$$${Since}\:\angle{CAB}=\mathrm{60}°,{we}\:{get}\:{from}\:{cosine}\: \\ $$$${rule}\:{thatEX}=\sqrt{\mathrm{10}}−\sqrt{\mathrm{5}} \\ $$$${Similarly},\:{we}\:{get}\:{that}\:{FY}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$${Observe}\:{that}\:{the}\:{circle}\:{circumscribes} \\ $$$${quadrilateral}\:{EXYF}\:{with}\:{sides} \\ $$$${EX}=\sqrt{\mathrm{10}}−\sqrt{\mathrm{5}},{XY}=\mathrm{4},{FY}=\mathrm{2}\sqrt{\mathrm{5}},{FE}=\mathrm{3} \\ $$$${The}\:{rest}\:{follows}\:{from}\:{Parameshvara}'{s} \\ $$$${circumradius}\:{formula}. \\ $$
Answered by mr W last updated on 29/Apr/23

Commented by Shlock last updated on 30/Apr/23
Very detailed, sir!
Commented by mr W last updated on 29/Apr/23

$${say}\:{AG}={x} \\ $$$${x}\left({x}+\mathrm{4}\right)=\mathrm{1}×\left(\mathrm{1}+\mathrm{3}\right) \\ $$$$\Rightarrow{x}=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2} \\ $$$${EF}=\sqrt{\mathrm{4}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{4}×\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\right)×\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{4}}=\frac{\mathrm{sin}\:\left(\alpha−\frac{\pi}{\mathrm{3}}\right)}{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\mathrm{3}−\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{2}}}} \\ $$$$\Rightarrow{R}=\frac{{EF}}{\mathrm{2}\:\mathrm{sin}\:\alpha}=\frac{\mathrm{2}\sqrt{\mathrm{5}}×\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{2}}}}{\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{15}\left(\mathrm{23}−\mathrm{6}\sqrt{\mathrm{2}}\right)}}{\mathrm{6}}\approx\mathrm{2}.\mathrm{459} \\ $$
