Question Number 5988 by sanusihammed last updated on 08/Jun/16
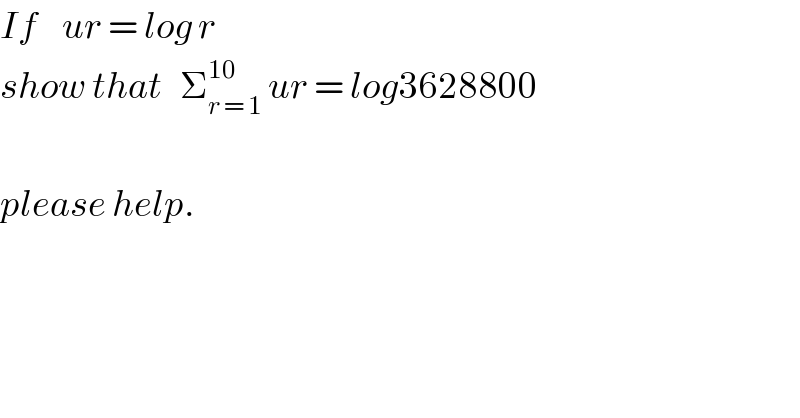
$${If}\:\:\:\:{ur}\:=\:{log}\:{r} \\ $$$${show}\:{that}\:\:\:\sum_{{r}\:=\:\mathrm{1}} ^{\mathrm{10}} \:{ur}\:=\:{log}\mathrm{3628800} \\ $$$$ \\ $$$${please}\:{help}. \\ $$
Answered by Yozzii last updated on 08/Jun/16

$${ur}={logr} \\ $$$$\therefore\underset{{r}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{ur}=\underset{{r}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{logr}={S} \\ $$$${For}\:{x},{y}>\mathrm{0}\:{we}\:{have}\:{that}\:{logx}+{logy}={logxy}. \\ $$$$ \\ $$$${PROOF}:\: \\ $$$${Let}\:{u}={a}^{{log}_{{a}} {m}} \:{where}\:{m}>\mathrm{0}\:\&\:{a}>\mathrm{0}.\Rightarrow{u}>\mathrm{0} \\ $$$${Also}\:{let}\:{n}={log}_{{a}} {r}^{{k}} \:\:\left({a}>\mathrm{0},{r}>\mathrm{0},{k}\neq\mathrm{0}\right)\Rightarrow{r}^{{k}} ={a}^{{n}} \Rightarrow{r}={a}^{{n}/{k}} \Rightarrow{log}_{{a}} {r}={n}/{k}\Rightarrow{n}={klog}_{{a}} {r}\:\:\left({Power}\:{rule}\right) \\ $$$$\Rightarrow{log}_{{a}} {u}={log}_{{a}} \left({a}^{{log}_{{a}} {m}} \right)=\left({log}_{{a}} {m}\right)\left({log}_{{a}} {a}\right) \\ $$$${Since}\:{a}={a}^{\mathrm{1}} \Rightarrow{log}_{{a}} {a}=\mathrm{1}. \\ $$$${log}_{{a}} {u}={log}_{{a}} {m}\Rightarrow{u}={m}\:\therefore\:{m}={a}^{{log}_{{a}} {m}} . \\ $$$${So},\:{if}\:{x},{y}>\mathrm{0}\Rightarrow\:{a}^{{log}_{{a}} {x}} ×{a}^{{log}_{{a}} {y}} ={xy}\:{or}\:{a}^{{log}_{{a}} {x}+{log}_{{a}} {y}} ={xy} \\ $$$$\Rightarrow{log}_{{a}} {xy}={log}_{{a}} {a}^{{log}_{{a}} {x}+{log}_{{a}} {y}} =\left({log}_{{a}} {x}+{log}_{{a}} {y}\right)\left({log}_{{a}} {a}\right)\:\:\:\:\: \\ $$$$\Rightarrow{log}_{{a}} {xy}={log}_{{a}} {x}+{log}_{{a}} {y}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$$ \\ $$$${Thus},\:{S}={log}\underset{{r}=\mathrm{1}} {\overset{\mathrm{10}} {\prod}}{r}={log}\left(\mathrm{10}!\right)={log}\mathrm{3628800} \\ $$
Commented by sanusihammed last updated on 08/Jun/16
$${Wow}\:{thanks}.\:{i}\:{really}\:{appreiate}= \\ $$
