Question Number 131552 by liberty last updated on 06/Feb/21
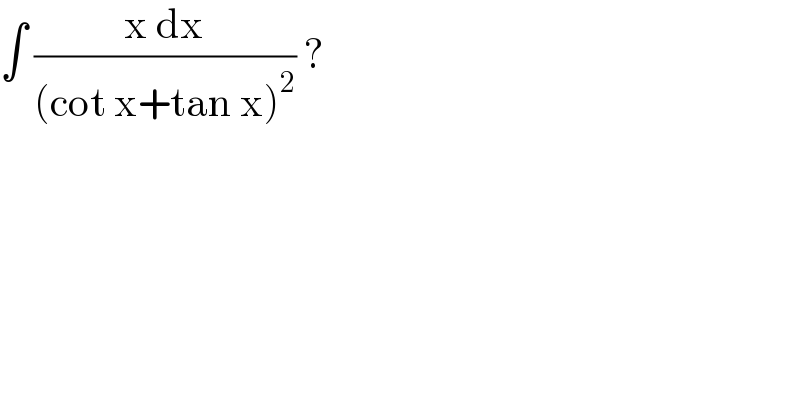
$$\int\:\frac{\mathrm{x}\:\mathrm{dx}}{\left(\mathrm{cot}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)^{\mathrm{2}} }\:? \\ $$
Answered by EDWIN88 last updated on 06/Feb/21
![⇔ cot x+tan x = (1/(sin x cos x)) = (2/(sin 2x)) ⇔ (1/((cot x+tan x)^2 ))=((sin^2 2x)/4) Now E=∫ ((x dx)/((cot x+tan x)^2 ))=(1/4)∫ xsin^2 2xdx E=(1/8)∫(x−xcos 4x)dx=(1/(16))x^2 −(1/8)∫x cos 4x dx E=(1/(16))x^2 −(1/8) [(1/4)x sin 4x −(1/4)∫ sin 4x dx ] E= (1/(16))x^2 −(1/(32))x sin 4x−(1/(128))cos 4x+c E=((8x^2 −4x sin 4x−cos 4x)/(128)) + c](https://www.tinkutara.com/question/Q131629.png)
$$\Leftrightarrow\:\mathrm{cot}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\:=\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{2x}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\left(\mathrm{cot}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)^{\mathrm{2}} }=\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}}{\mathrm{4}} \\ $$$$\mathrm{Now}\:\mathrm{E}=\int\:\frac{\mathrm{x}\:\mathrm{dx}}{\left(\mathrm{cot}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\int\:\mathrm{xsin}\:^{\mathrm{2}} \mathrm{2xdx} \\ $$$$\mathrm{E}=\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{x}−\mathrm{xcos}\:\mathrm{4x}\right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{16}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{x}\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{dx} \\ $$$$\mathrm{E}=\frac{\mathrm{1}}{\mathrm{16}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}\:\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}\:\mathrm{sin}\:\mathrm{4x}\:−\frac{\mathrm{1}}{\mathrm{4}}\int\:\mathrm{sin}\:\mathrm{4x}\:\mathrm{dx}\:\right] \\ $$$$\mathrm{E}=\:\frac{\mathrm{1}}{\mathrm{16}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{32}}\mathrm{x}\:\mathrm{sin}\:\mathrm{4x}−\frac{\mathrm{1}}{\mathrm{128}}\mathrm{cos}\:\mathrm{4x}+\mathrm{c} \\ $$$$\mathrm{E}=\frac{\mathrm{8x}^{\mathrm{2}} −\mathrm{4x}\:\mathrm{sin}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{4x}}{\mathrm{128}}\:+\:\mathrm{c}\: \\ $$
