Menu Close

dx-1-x-2-3-2-solve-this-pls-

Tinku Tara 0 Comments
Pin




Question Number 60944 by pooja24 last updated on 27/May/19
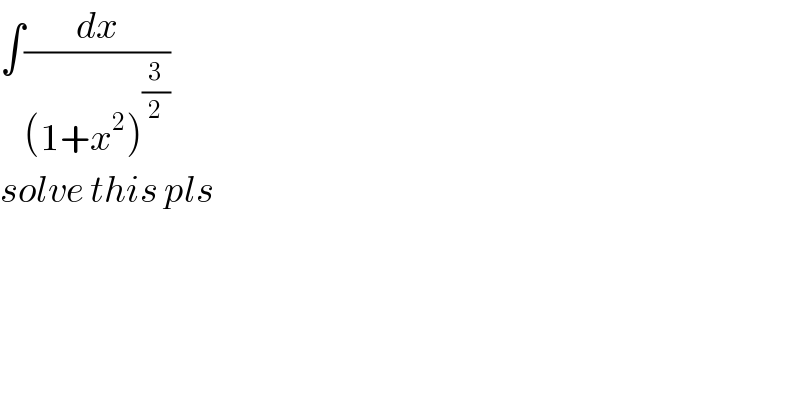
∫(dx/((1+x^2 )^(3/2) )) solve this pls
$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${solve}\:{this}\:{pls} \\ $$
Commented by maxmathsup by imad last updated on 27/May/19
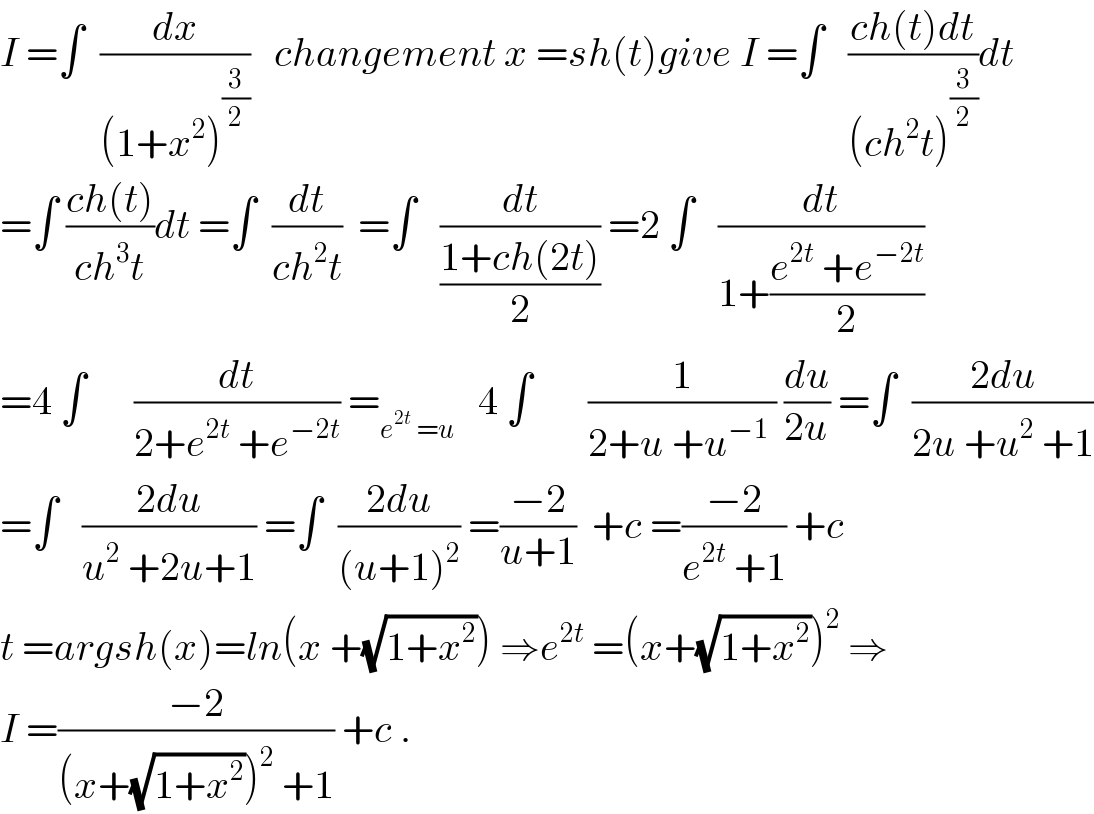
I =∫ (dx/((1+x^2 )^(3/2) )) changement x =sh(t)give I =∫ ((ch(t)dt)/((ch^2 t)^(3/2) ))dt =∫ ((ch(t))/(ch^3 t))dt =∫ (dt/(ch^2 t)) =∫ (dt/((1+ch(2t))/2)) =2 ∫ (dt/(1+((e^(2t) +e^(−2t) )/2))) =4 ∫ (dt/(2+e^(2t) +e^(−2t) )) =_(e^(2t) =u) 4 ∫ (1/(2+u +u^(−1) )) (du/(2u)) =∫ ((2du)/(2u +u^2 +1)) =∫ ((2du)/(u^2 +2u+1)) =∫ ((2du)/((u+1)^2 )) =((−2)/(u+1)) +c =((−2)/(e^(2t) +1)) +c t =argsh(x)=ln(x +(√(1+x^2 ))) ⇒e^(2t) =(x+(√(1+x^2 )))^2 ⇒ I =((−2)/((x+(√(1+x^2 )))^2 +1)) +c .
$${I}\:=\int\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:\:{changement}\:{x}\:={sh}\left({t}\right){give}\:{I}\:=\int\:\:\:\frac{{ch}\left({t}\right){dt}}{\left({ch}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt} \\ $$$$=\int\:\frac{{ch}\left({t}\right)}{{ch}^{\mathrm{3}} {t}}{dt}\:=\int\:\:\frac{{dt}}{{ch}^{\mathrm{2}} {t}}\:\:=\int\:\:\:\frac{{dt}}{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}\:=\mathrm{2}\:\int\:\:\:\frac{{dt}}{\mathrm{1}+\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}} \\ $$$$=\mathrm{4}\:\int\:\:\:\:\:\:\frac{{dt}}{\mathrm{2}+{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }\:=_{{e}^{\mathrm{2}{t}} \:={u}} \:\:\:\mathrm{4}\:\int\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}+{u}\:+{u}^{−\mathrm{1}} \:}\:\frac{{du}}{\mathrm{2}{u}}\:=\int\:\:\frac{\mathrm{2}{du}}{\mathrm{2}{u}\:+{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\int\:\:\:\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}{u}+\mathrm{1}}\:=\int\:\:\frac{\mathrm{2}{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}}{{u}+\mathrm{1}}\:\:+{c}\:=\frac{−\mathrm{2}}{{e}^{\mathrm{2}{t}} \:+\mathrm{1}}\:+{c} \\ $$$${t}\:={argsh}\left({x}\right)={ln}\left({x}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:\Rightarrow{e}^{\mathrm{2}{t}} \:=\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\frac{−\mathrm{2}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \:+\mathrm{1}}\:+{c}\:. \\ $$
Answered by tanmay last updated on 27/May/19
x=tana dx=sec^2 ada ∫((sec^2 ada)/((sec^2 a)^(3/2) )) ∫(da/(seca)) ∫cosada sina+c =(x/( (√(x^2 +1)) ))+c
$${x}={tana}\:\:\:{dx}={sec}^{\mathrm{2}} {ada} \\ $$$$\int\frac{{sec}^{\mathrm{2}} {ada}}{\left({sec}^{\mathrm{2}} {a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\int\frac{{da}}{{seca}} \\ $$$$\int{cosada} \\ $$$${sina}+{c} \\ $$$$=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:}+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *