Question Number 192112 by Spillover last updated on 08/May/23
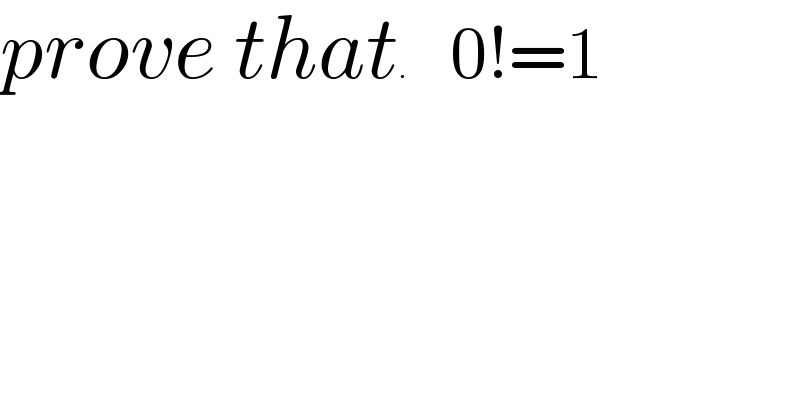
$${prove}\:{that}.\:\:\:\:\:\:\:\mathrm{0}!=\mathrm{1} \\ $$
Commented by Frix last updated on 08/May/23
![I think it′s defined 0!=1 There′s the idea of the “Empty Product” It′s obvious that the “Empty Sum”=0 because if we sum up nothing we still have nothing. Because the sum log x +log y =log xy we set the “Empty Product”=1 x!=Π_(k=1) ^x ⇒ 0! is the “Empty Product” But we can simply calculate backwards 3!=6 2!=((3!)/3)=2 1!=((2!)/2)=1 0!=((1!)/1)=1 [⇒ x! is not defined for x∈Z^− ]](https://www.tinkutara.com/question/Q192121.png)
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{defined}\:\mathrm{0}!=\mathrm{1}\: \\ $$$$\mathrm{There}'\mathrm{s}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{of}\:\mathrm{the}\:“\mathrm{Empty}\:\mathrm{Product}'' \\ $$$$\:\:\:\:\:\mathrm{It}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{that}\:\mathrm{the}\:“\mathrm{Empty}\:\mathrm{Sum}''=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{because}\:\mathrm{if}\:\mathrm{we}\:\mathrm{sum}\:\mathrm{up}\:\mathrm{nothing}\:\mathrm{we}\:\mathrm{still} \\ $$$$\:\:\:\:\:\mathrm{have}\:\mathrm{nothing}.\:\mathrm{Because}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\:\:\:\:\:\mathrm{log}\:{x}\:+\mathrm{log}\:{y}\:=\mathrm{log}\:{xy}\:\mathrm{we}\:\mathrm{set}\:\mathrm{the}\:“\mathrm{Empty} \\ $$$$\:\:\:\:\:\mathrm{Product}''=\mathrm{1} \\ $$$$\:\:\:\:\:{x}!=\underset{{k}=\mathrm{1}} {\overset{{x}} {\prod}}\:\Rightarrow\:\mathrm{0}!\:\mathrm{is}\:\mathrm{the}\:“\mathrm{Empty}\:\mathrm{Product}'' \\ $$$$ \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{we}\:\mathrm{can}\:\mathrm{simply}\:\mathrm{calculate}\:\mathrm{backwards} \\ $$$$\mathrm{3}!=\mathrm{6} \\ $$$$\mathrm{2}!=\frac{\mathrm{3}!}{\mathrm{3}}=\mathrm{2} \\ $$$$\mathrm{1}!=\frac{\mathrm{2}!}{\mathrm{2}}=\mathrm{1} \\ $$$$\mathrm{0}!=\frac{\mathrm{1}!}{\mathrm{1}}=\mathrm{1} \\ $$$$\left[\Rightarrow\:{x}!\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{Z}^{−} \right] \\ $$
Commented by Spillover last updated on 12/May/23

$${thanks}\: \\ $$
Answered by Skabetix last updated on 08/May/23
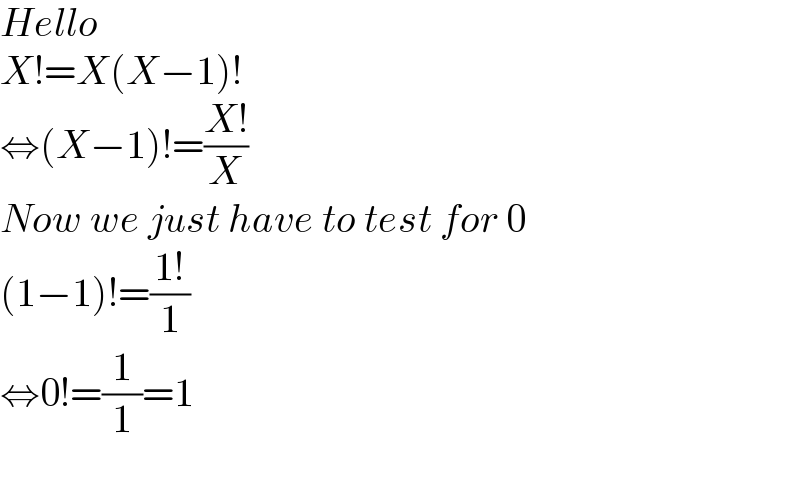
$${Hello} \\ $$$${X}!={X}\left({X}−\mathrm{1}\right)! \\ $$$$\Leftrightarrow\left({X}−\mathrm{1}\right)!=\frac{{X}!}{{X}} \\ $$$${Now}\:{we}\:{just}\:{have}\:{to}\:{test}\:{for}\:\mathrm{0} \\ $$$$\left(\mathrm{1}−\mathrm{1}\right)!=\frac{\mathrm{1}!}{\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{0}!=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$$ \\ $$
Answered by Spillover last updated on 12/May/23
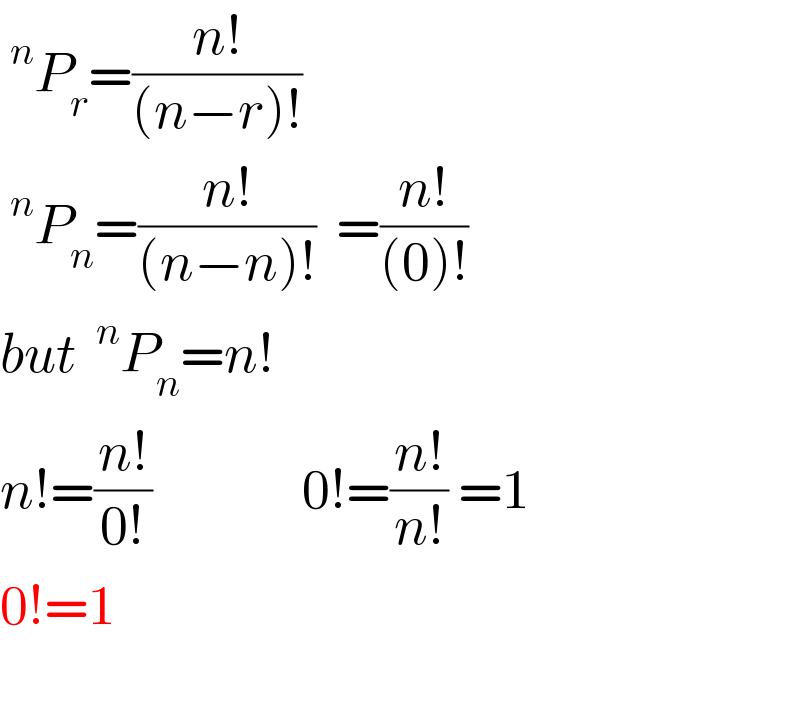
$$\:^{{n}} {P}_{{r}} =\frac{{n}!}{\left({n}−{r}\right)!}\:\:\:\:\: \\ $$$$\:^{{n}} {P}_{{n}} =\frac{{n}!}{\left({n}−{n}\right)!}\:\:=\frac{{n}!}{\left(\mathrm{0}\right)!}\:\:\:\: \\ $$$${but}\:\:^{{n}} {P}_{{n}} ={n}! \\ $$$${n}!=\frac{{n}!}{\mathrm{0}!}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}!=\frac{{n}!}{{n}!}\:=\mathrm{1}\: \\ $$$$\mathrm{0}!=\mathrm{1} \\ $$$$ \\ $$
