Menu Close

The-2nd-4th-and-8th-term-of-an-AP-are-the-consecutive-term-of-a-GP-If-the-sum-of-the-3rd-and-4th-term-of-the-AP-is-20-Find-the-sum-of-the-first-four-terms-of-the-AP-

Tinku Tara 0 Comments
Pin




Question Number 61117 by Tawa1 last updated on 29/May/19
The 2nd, 4th and 8th term of an AP are the consecutive term of a GP. If the sum of the 3rd and 4th term of the AP is 20. Find the sum of the first four terms of the AP.
$$\mathrm{The}\:\mathrm{2nd},\:\mathrm{4th}\:\mathrm{and}\:\mathrm{8th}\:\mathrm{term}\:\mathrm{of}\:\mathrm{an}\:\mathrm{AP}\:\mathrm{are}\:\mathrm{the}\:\mathrm{consecutive}\:\mathrm{term}\:\mathrm{of}\:\mathrm{a}\:\mathrm{GP}. \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3rd}\:\mathrm{and}\:\mathrm{4th}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{AP}\:\mathrm{is}\:\mathrm{20}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{four}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{AP}. \\ $$
Answered by Kunal12588 last updated on 29/May/19
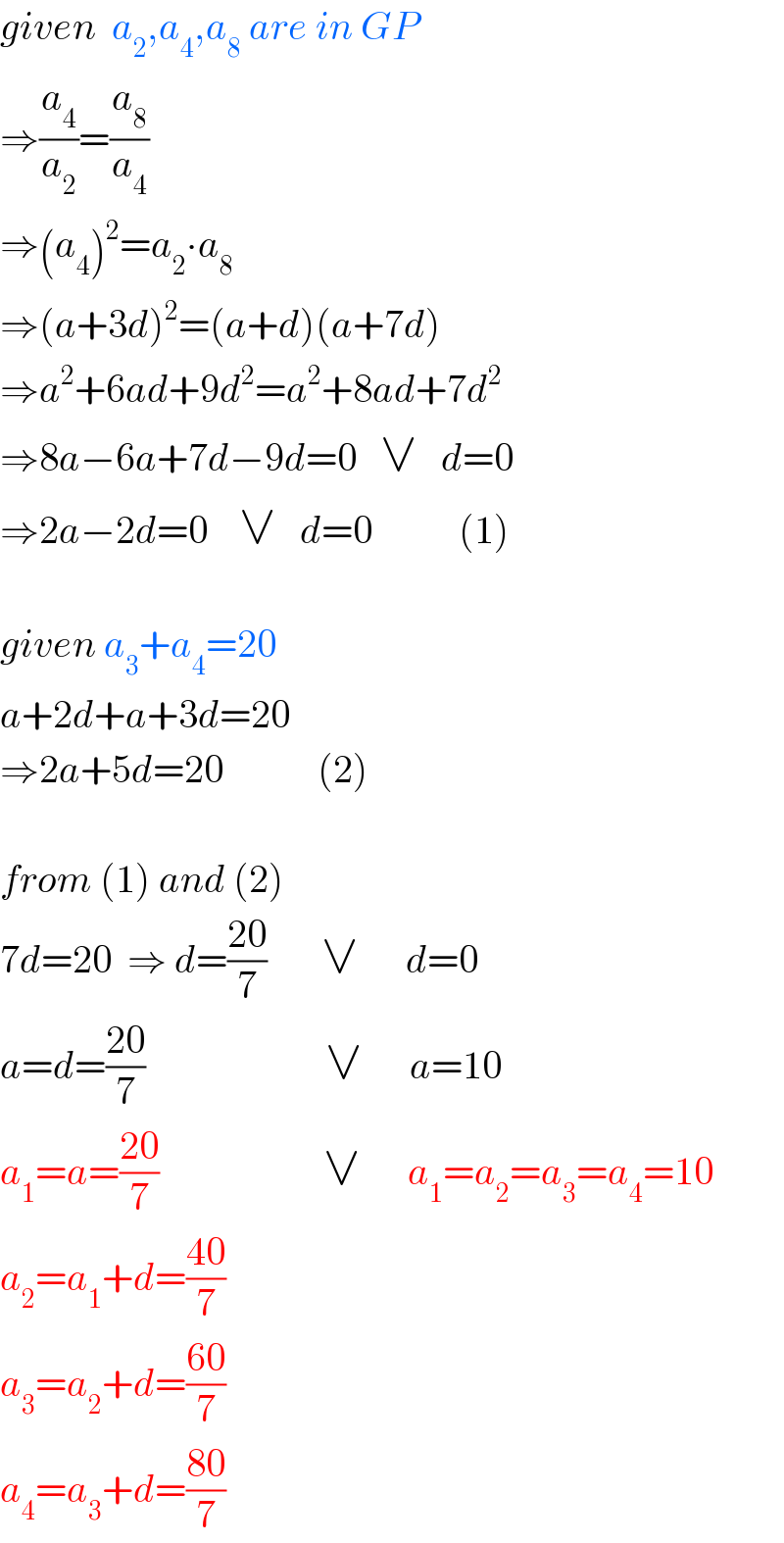
given a_2 ,a_4 ,a_8 are in GP ⇒(a_4 /a_2 )=(a_8 /a_4 ) ⇒(a_4 )^2 =a_2 ∙a_8 ⇒(a+3d)^2 =(a+d)(a+7d) ⇒a^2 +6ad+9d^2 =a^2 +8ad+7d^2 ⇒8a−6a+7d−9d=0 ∨ d=0 ⇒2a−2d=0 ∨ d=0 (1) given a_3 +a_4 =20 a+2d+a+3d=20 ⇒2a+5d=20 (2) from (1) and (2) 7d=20 ⇒ d=((20)/7) ∨ d=0 a=d=((20)/7) ∨ a=10 a_1 =a=((20)/7) ∨ a_1 =a_2 =a_3 =a_4 =10 a_2 =a_1 +d=((40)/7) a_3 =a_2 +d=((60)/7) a_4 =a_3 +d=((80)/7)
$${given}\:\:{a}_{\mathrm{2}} ,{a}_{\mathrm{4}} ,{a}_{\mathrm{8}} \:{are}\:{in}\:{GP} \\ $$$$\Rightarrow\frac{{a}_{\mathrm{4}} }{{a}_{\mathrm{2}} }=\frac{{a}_{\mathrm{8}} }{{a}_{\mathrm{4}} } \\ $$$$\Rightarrow\left({a}_{\mathrm{4}} \right)^{\mathrm{2}} ={a}_{\mathrm{2}} \centerdot{a}_{\mathrm{8}} \\ $$$$\Rightarrow\left({a}+\mathrm{3}{d}\right)^{\mathrm{2}} =\left({a}+{d}\right)\left({a}+\mathrm{7}{d}\right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\mathrm{6}{ad}+\mathrm{9}{d}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{8}{ad}+\mathrm{7}{d}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{8}{a}−\mathrm{6}{a}+\mathrm{7}{d}−\mathrm{9}{d}=\mathrm{0}\:\:\:\vee\:\:\:{d}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{a}−\mathrm{2}{d}=\mathrm{0}\:\:\:\:\vee\:\:\:{d}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right)\:\:\:\:\: \\ $$$$ \\ $$$${given}\:{a}_{\mathrm{3}} +{a}_{\mathrm{4}} =\mathrm{20} \\ $$$${a}+\mathrm{2}{d}+{a}+\mathrm{3}{d}=\mathrm{20} \\ $$$$\Rightarrow\mathrm{2}{a}+\mathrm{5}{d}=\mathrm{20}\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$${from}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{7}{d}=\mathrm{20}\:\:\Rightarrow\:{d}=\frac{\mathrm{20}}{\mathrm{7}}\:\:\:\:\:\:\:\vee\:\:\:\:\:\:{d}=\mathrm{0} \\ $$$${a}={d}=\frac{\mathrm{20}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\:\:\:\:\:\:{a}=\mathrm{10}\:\:\:\: \\ $$$${a}_{\mathrm{1}} ={a}=\frac{\mathrm{20}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\:\:\:\:\:\:{a}_{\mathrm{1}} ={a}_{\mathrm{2}} ={a}_{\mathrm{3}} ={a}_{\mathrm{4}} =\mathrm{10} \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}} +{d}=\frac{\mathrm{40}}{\mathrm{7}} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{2}} +{d}=\frac{\mathrm{60}}{\mathrm{7}} \\ $$$${a}_{\mathrm{4}} ={a}_{\mathrm{3}} +{d}=\frac{\mathrm{80}}{\mathrm{7}} \\ $$
Commented by Tawa1 last updated on 29/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 29/May/19
AnOther Way a_2 ,a_4 ,a_8 =a,ar,ar^2 [∵ a_2 ,a_4 ,a_8 are in GP] a_4 −a_2 =ar−a=2d⇒d=((ar−a)/2) a_8 −a_4 =ar^2 −ar=4d⇒d=((ar^2 −ar)/4) ((ar−a)/2)=((ar^2 −ar)/4) 2r−2=r^2 −r r^2 −3r+2=0⇒r=1,2 ∴ r=2 [r≠1 in a GP] ∴d=((ar−a)/2)=((2a−a)/2)=(a/2) Now a_3 +a_4 =20 [Given] (a_2 +d)+ar=20 (a+(a/2))+a(2)=20 2a+a+4a=40 a=((40)/7)⇒d=(a/2)=((20)/7) a_1 +a_2 +a_3 +a_4 =(a−d)+a+20=2a−d+20 =2(((40)/7))−((20)/7)+20 =((80−20+140)/7)=((200)/7)
$$\mathrm{AnOther}\:\mathrm{Way} \\ $$$$\:\:\:\:\mathrm{a}_{\mathrm{2}} ,\mathrm{a}_{\mathrm{4}} ,\mathrm{a}_{\mathrm{8}} ={a},{ar},{ar}^{\mathrm{2}} \:\left[\because\:\mathrm{a}_{\mathrm{2}} ,\mathrm{a}_{\mathrm{4}} ,\mathrm{a}_{\mathrm{8}} \:\mathrm{are}\:\mathrm{in}\:\mathrm{GP}\right] \\ $$$$\:\:\:\mathrm{a}_{\mathrm{4}} −\mathrm{a}_{\mathrm{2}} ={ar}−{a}=\mathrm{2}{d}\Rightarrow{d}=\frac{{ar}−{a}}{\mathrm{2}} \\ $$$$\:\:\:\mathrm{a}_{\mathrm{8}} −\mathrm{a}_{\mathrm{4}} ={ar}^{\mathrm{2}} −{ar}=\mathrm{4}{d}\Rightarrow{d}=\frac{{ar}^{\mathrm{2}} −{ar}}{\mathrm{4}} \\ $$$$\:\:\:\:\frac{{ar}−{a}}{\mathrm{2}}=\frac{{ar}^{\mathrm{2}} −{ar}}{\mathrm{4}} \\ $$$$\:\:\:\mathrm{2}{r}−\mathrm{2}={r}^{\mathrm{2}} −{r} \\ $$$$\:\:\:\:{r}^{\mathrm{2}} −\mathrm{3}{r}+\mathrm{2}=\mathrm{0}\Rightarrow{r}=\mathrm{1},\mathrm{2} \\ $$$$\therefore\:{r}=\mathrm{2}\:\:\:\:\:\:\:\:\:\left[{r}\neq\mathrm{1}\:\mathrm{in}\:\mathrm{a}\:\mathrm{GP}\right] \\ $$$$\therefore{d}=\frac{{ar}−{a}}{\mathrm{2}}=\frac{\mathrm{2}{a}−{a}}{\mathrm{2}}=\frac{{a}}{\mathrm{2}} \\ $$$$\mathrm{Now}\:\:\mathrm{a}_{\mathrm{3}} +\mathrm{a}_{\mathrm{4}} =\mathrm{20}\:\:\left[\mathrm{Given}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{a}_{\mathrm{2}} +{d}\right)+{ar}=\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({a}+\frac{{a}}{\mathrm{2}}\right)+{a}\left(\mathrm{2}\right)=\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{a}+{a}+\mathrm{4}{a}=\mathrm{40} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\frac{\mathrm{40}}{\mathrm{7}}\Rightarrow{d}=\frac{{a}}{\mathrm{2}}=\frac{\mathrm{20}}{\mathrm{7}} \\ $$$$ \\ $$$$\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} +\mathrm{a}_{\mathrm{3}} +\mathrm{a}_{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:=\left({a}−{d}\right)+{a}+\mathrm{20}=\mathrm{2}{a}−{d}+\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\frac{\mathrm{40}}{\mathrm{7}}\right)−\frac{\mathrm{20}}{\mathrm{7}}+\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{80}−\mathrm{20}+\mathrm{140}}{\mathrm{7}}=\frac{\mathrm{200}}{\mathrm{7}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *