Menu Close

calculus-evaluate-0-1-1-x-4-ln-x-1-x-6-dx-

Tinku Tara 0 Comments
Pin




Question Number 126661 by mnjuly1970 last updated on 23/Dec/20
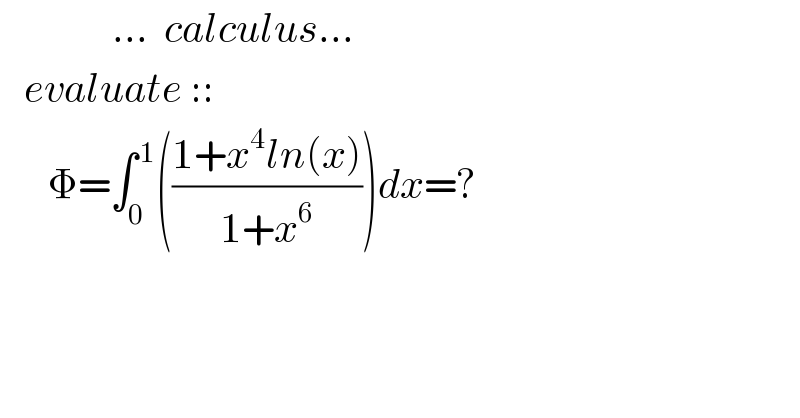
... calculus... evaluate :: Φ=∫_0 ^( 1) (((1+x^4 ln(x))/(1+x^6 )))dx=?
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:\:{calculus}… \\ $$$$\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\Phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}+{x}^{\mathrm{4}} {ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{6}} }\right){dx}=? \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 23/Dec/20
∫_0 ^1 ((1+x^4 log(x))/(1+x^6 ))dx logx=t =∫_(−∞) ^0 ((1+e^(4t) t)/(1+e^(6t) ))e^t dt t=−u =∫_0 ^∞ ((1−e^(−4u) u)/(1+e^(−6u) ))e^(−u) du=∫_0 ^∞ ((e^(5u) −e^u u)/(1+e^(6u) ))du =Σ_(n=1) ^∞ (−1)^(n+1) ∫_0 ^∞ e^(−6un+5u) −∫_0 ^∞ ue^(−6un+u) du =Σ_(n=1) ^∞ (−1)^(n+1) (1/((6n−5)))−Σ_(n=1) ^∞ (−1)^(n+1) (1/((6n−1)^2 )) =Σ_(n=0) ^∞ (−1)^n ((1/((6n+1)))−(1/((6n+5)^2 )))=(1−(1/7)+(1/(13))−(1/(17))+...)−(1/5^2 )+(1/(11^2 ))−. Σ_(n=0) ^∞ (((−1)^n )/(6n+1))=(π/6)−(1/( (√3)))log((((√3)+1)/( 2))) Σ_(n=0) ^∞ (((−1)^n )/((6n+5)^2 ))=(1/(36))Σ_(n=0) ^∞ (((−1)^n )/((n+(5/6))^2 ))=(1/(144))(ψ^1 ((5/(12)))−ψ^1 (((11)/(12))))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+{x}^{\mathrm{4}} {log}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:\:\:\:\:\:\:\:\:{logx}={t} \\ $$$$=\int_{−\infty} ^{\mathrm{0}} \frac{\mathrm{1}+{e}^{\mathrm{4}{t}} {t}}{\mathrm{1}+{e}^{\mathrm{6}{t}} }{e}^{{t}} {dt}\:\:\:\:\:\:\:\:\:\:\:{t}=−{u} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{e}^{−\mathrm{4}{u}} {u}}{\mathrm{1}+{e}^{−\mathrm{6}{u}} }{e}^{−{u}} {du}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{\mathrm{5}{u}} −{e}^{{u}} {u}}{\mathrm{1}+{e}^{\mathrm{6}{u}} }{du} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{6}{un}+\mathrm{5}{u}} −\int_{\mathrm{0}} ^{\infty} {ue}^{−\mathrm{6}{un}+{u}} {du} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{6}{n}−\mathrm{5}\right)}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{6}{n}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\left(\mathrm{6}{n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left(\mathrm{6}{n}+\mathrm{5}\right)^{\mathrm{2}} }\right)=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{17}}+…\right)−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }−. \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{6}{n}+\mathrm{1}}=\frac{\pi}{\mathrm{6}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{log}\left(\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\mathrm{2}}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{6}{n}+\mathrm{5}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{144}}\left(\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{12}}\right)−\psi^{\mathrm{1}} \left(\frac{\mathrm{11}}{\mathrm{12}}\right)\right) \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 23/Dec/20
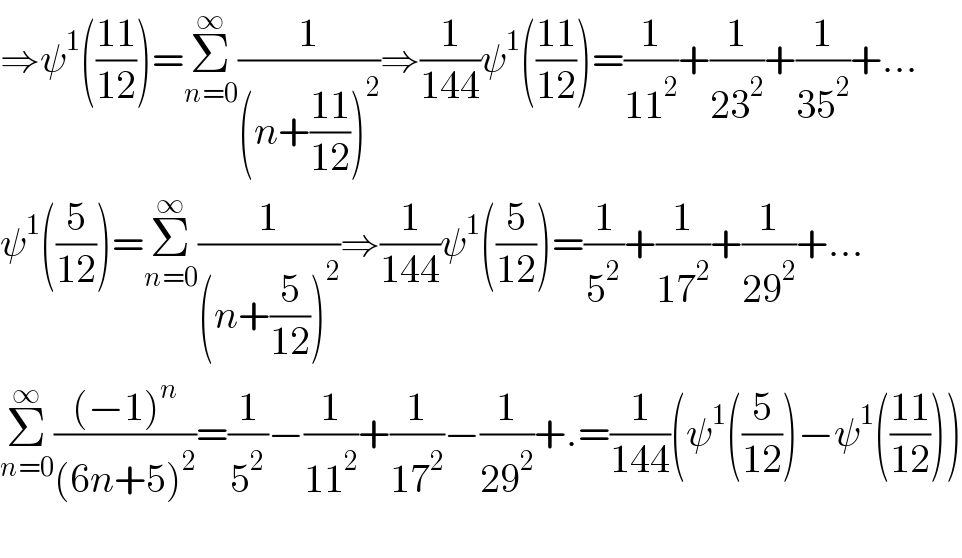
⇒ψ^1 (((11)/(12)))=Σ_(n=0) ^∞ (1/((n+((11)/(12)))^2 ))⇒(1/(144))ψ^1 (((11)/(12)))=(1/(11^2 ))+(1/(23^2 ))+(1/(35^2 ))+... ψ^1 ((5/(12)))=Σ_(n=0) ^∞ (1/((n+(5/(12)))^2 ))⇒(1/(144))ψ^1 ((5/(12)))=(1/5^2 )+(1/(17^2 ))+(1/(29^2 ))+... Σ_(n=0) ^∞ (((−1)^n )/((6n+5)^2 ))=(1/5^2 )−(1/(11^2 ))+(1/(17^2 ))−(1/(29^2 ))+.=(1/(144))(ψ^1 ((5/(12)))−ψ^1 (((11)/(12))))
$$\Rightarrow\psi^{\mathrm{1}} \left(\frac{\mathrm{11}}{\mathrm{12}}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{11}}{\mathrm{12}}\right)^{\mathrm{2}} }\Rightarrow\frac{\mathrm{1}}{\mathrm{144}}\psi^{\mathrm{1}} \left(\frac{\mathrm{11}}{\mathrm{12}}\right)=\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{23}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{35}^{\mathrm{2}} }+… \\ $$$$\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{12}}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{5}}{\mathrm{12}}\right)^{\mathrm{2}} }\Rightarrow\frac{\mathrm{1}}{\mathrm{144}}\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{12}}\right)=\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{17}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{29}^{\mathrm{2}} }+… \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{6}{n}+\mathrm{5}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{17}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{29}^{\mathrm{2}} }+.=\frac{\mathrm{1}}{\mathrm{144}}\left(\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{12}}\right)−\psi^{\mathrm{1}} \left(\frac{\mathrm{11}}{\mathrm{12}}\right)\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 23/Dec/20
thank you so much...
$${thank}\:{you}\:{so}\:{much}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *