Question Number 66018 by Rio Michael last updated on 07/Aug/19
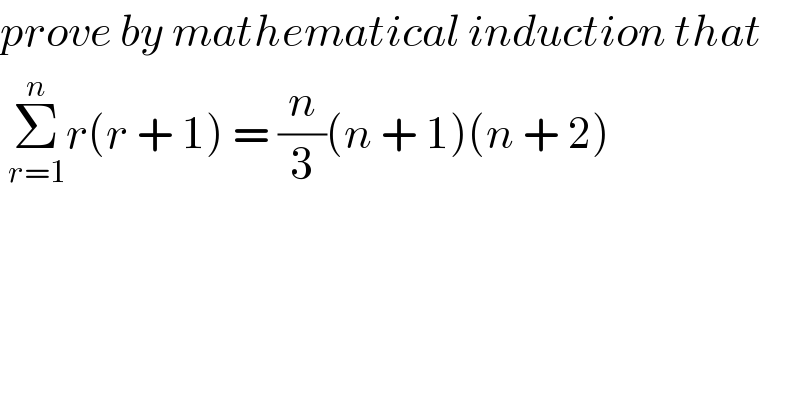
$${prove}\:{by}\:{mathematical}\:{induction}\:{that}\: \\ $$$$\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}\left({r}\:+\:\mathrm{1}\right)\:=\:\frac{{n}}{\mathrm{3}}\left({n}\:+\:\mathrm{1}\right)\left({n}\:+\:\mathrm{2}\right) \\ $$
Commented by Prithwish sen last updated on 07/Aug/19
![when n=1 1(1+1)=(1/3)(1+1)(1+2) 2=2 it is true for n=1 for n=2 1(1+1)+2(2+1)=(2/3)(2+1)(2+2) 8=8 it is true for n=2 Now let us assume it is true for n=k i.e Σ_(r=1) ^k r(r+1) = (k/3)(k+1)(k+2) ⇒1(1+1)+2(2+1)+...k(k+1)=(k/3)(k+1)(k+2) now for n=k+1 Σ_(r=1) ^(k+1) r(r+1)=1(1+1)+2(2+1)+....+k(k+1)+(k+1)(k+2) =(k/3)(k+1)(k+2)+(k+1)(k+2)=(k+1)(k+2)((k/3)+1) =(((k+1))/3)[(k+1)+1][(k+1)+2] ∴ it is true for n=k+1 also. Hence proved.](https://www.tinkutara.com/question/Q66022.png)
$$\mathrm{when}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{1}\left(\mathrm{1}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{2}\right) \\ $$$$\mathrm{2}=\mathrm{2}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{n}=\mathrm{2} \\ $$$$\mathrm{1}\left(\mathrm{1}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{2}+\mathrm{1}\right)=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{2}+\mathrm{2}\right) \\ $$$$\mathrm{8}=\mathrm{8}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{2} \\ $$$$\mathrm{Now}\:\mathrm{let}\:\mathrm{us}\:\mathrm{assume}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k} \\ $$$$\mathrm{i}.\mathrm{e} \\ $$$$\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{r}\left(\mathrm{r}+\mathrm{1}\right)\:=\:\frac{\mathrm{k}}{\mathrm{3}}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{1}\left(\mathrm{1}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{2}+\mathrm{1}\right)+…\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)=\frac{\mathrm{k}}{\mathrm{3}}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right) \\ $$$$\mathrm{now}\:\mathrm{for}\:\mathrm{n}=\mathrm{k}+\mathrm{1} \\ $$$$\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{k}+\mathrm{1}} {\sum}}\mathrm{r}\left(\mathrm{r}+\mathrm{1}\right)=\mathrm{1}\left(\mathrm{1}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{2}+\mathrm{1}\right)+….+\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)+\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right) \\ $$$$=\frac{\mathrm{k}}{\mathrm{3}}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)+\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)=\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)\left(\frac{\mathrm{k}}{\mathrm{3}}+\mathrm{1}\right) \\ $$$$=\frac{\left(\mathrm{k}+\mathrm{1}\right)}{\mathrm{3}}\left[\left(\mathrm{k}+\mathrm{1}\right)+\mathrm{1}\right]\left[\left(\mathrm{k}+\mathrm{1}\right)+\mathrm{2}\right] \\ $$$$\therefore\:\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k}+\mathrm{1}\:\mathrm{also}. \\ $$$$\mathrm{Hence}\:\mathrm{proved}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Tanmay chaudhury last updated on 07/Aug/19

$$\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{3}+\mathrm{3}.\mathrm{4}+…+{n}\left({n}+\mathrm{1}\right)=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$$${n}=\mathrm{1} \\ $$$${LHS}=\mathrm{1}×\mathrm{2}=\mathrm{2} \\ $$$${RHS}=\frac{\mathrm{1}\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{2}\right)}{\mathrm{3}}=\mathrm{2} \\ $$$${LHS}={RHS} \\ $$$${n}=\mathrm{2} \\ $$$${LHS}=\mathrm{1}×\mathrm{2}+\mathrm{2}×\mathrm{3}=\mathrm{8} \\ $$$${RHS}=\frac{\mathrm{2}\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{2}+\mathrm{2}\right)}{\mathrm{3}}=\mathrm{8} \\ $$$${LHS}={RHS} \\ $$$${now}\:{assume}\:{when}\:{n}={k}\:{given}\:{statement}\:{is}\:{true} \\ $$$${we}\:{have}\:{prove}\:\:{that}\:{it}\:{is}\:{true}\:{n}={k}+\mathrm{1} \\ $$$$\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{3}+\mathrm{3}.\mathrm{4}+…+{k}\left({k}+\mathrm{1}\right)=\frac{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\mathrm{3}} \\ $$$${now}\:{LHS} \\ $$$$\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{3}+\mathrm{3}.\mathrm{4}+..+{k}\left({k}+\mathrm{1}\right)+\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right) \\ $$$$\left.=\frac{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\mathrm{3}}+\left({k}+\mathrm{1}\right)\left({k}\right)\mathrm{2}\right) \\ $$$$=\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left(\frac{{k}}{\mathrm{3}}+\mathrm{1}\right) \\ $$$$=\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left({k}+\mathrm{3}\right)}{\mathrm{3}} \\ $$$${RHS} \\ $$$$=\frac{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right.}{\mathrm{3}}+\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right) \\ $$$$=\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\mathrm{1}}×\left(\frac{{k}}{\mathrm{3}}+\mathrm{1}\right) \\ $$$$=\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left({k}+\mathrm{3}\right)}{\mathrm{3}} \\ $$$${LHS}={RHS}\:\:\left[{hence}\:{proved}\right. \\ $$
Commented by Rio Michael last updated on 07/Aug/19

$${thank}\:{y}'{all} \\ $$
